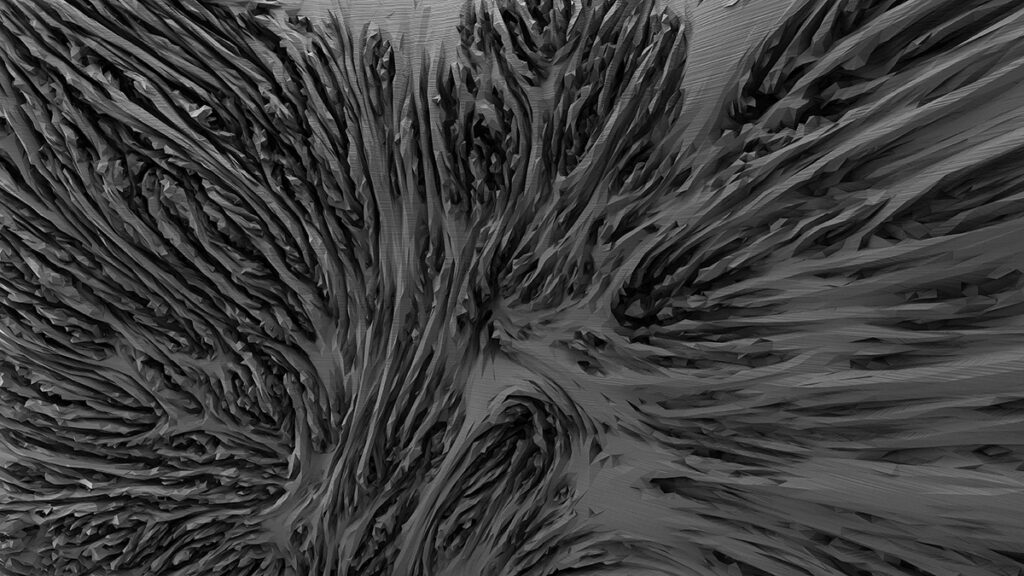
Intro
About in 2016, accidently by a workshop held in CAFA, Chritoph Klemmt presented his research on Cell Based Venation Systems and works from Andy Lomas and Deskriptiv, since then I was deeply attracted by generative form and beauty of self-organizing – in which Differential Growth – a typical algorithm took far-reaching impact on my thinking. It pushes me forward, to work on it and several complex systems such as Reaction Diffusion and Multi Agent system – which finally inspired my experiment “Self-Organizing of Basic Behaviors” . Despite the resources about Differential Growth is in shortage on Chinese websites and information about this word is mainly medical and biological – rather than geometrical – I will give a short introduction on this algorithm – Differential Growth.
#1 Definition
Biological definition of Differential Growth is shown below:
different rates of growth in associated tissues or structures; used especially in embryology when the differences in growth rates result in changing the original proportions or relations.
——Farlex Partner Medical Dictionary © Farlex 2012
What we are going to talk about today is geometrical – which is a little bit different from ” different rates of growth in associated tissues or structures ” above – it is just like its literal meaning – by enlarging differencesto to develop complex form. It’s a rule of developing utilization and complexity in limited space by wrinking and folding. Just like the brain folds to growth more neurons, gut folds to absorb nutritions, and chip folds to store more data……
In my opinion, Differential Growth is a dynamic balance between behaviors, a process generated complex forms.
About Differential Growth, there was a book called “The Algorithmic Beauty of Seaweeds, Sponges and Coral” – which well included researches on several undersea creatures, and some of them – some corals growth in a typical Differential way.


Differential Growth describes a surface that grows at different rates in different locations. Biological systems can create complex forms from the interaction of physical properties of a surface and simple controls of growth rates over time.
——Nervous System
Differential Growth always mentioned the factor of “nutrition” (well implemented by Andy Lomas and medical definition above) – a weight of growth rate. But the weight is neither man-made nor another set of rule – actually it’s a property of geometry itself. Basically, the “nutrition” is the curvature of geometry, which is exactly the “difference” in Differential Growth. During the process, it’s clear that the whole algorithm always follows a rule of enlarging curvature and expanding – depression becomes “gap” and bulge becomes “branches”. Any trivial difference will be extraordinarily enlarged after iterations.

#2 Examples
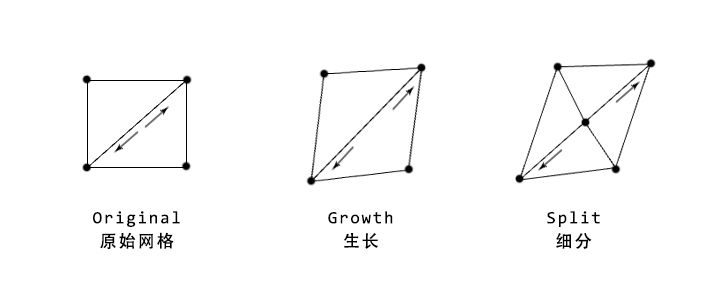
Differential Growth has approximately three derivatives: 2D-Splitting, Triangular-Splitting and Hexagonal-Splitting. In this post, we mainly discuss on latter two types.
2D-Splitting
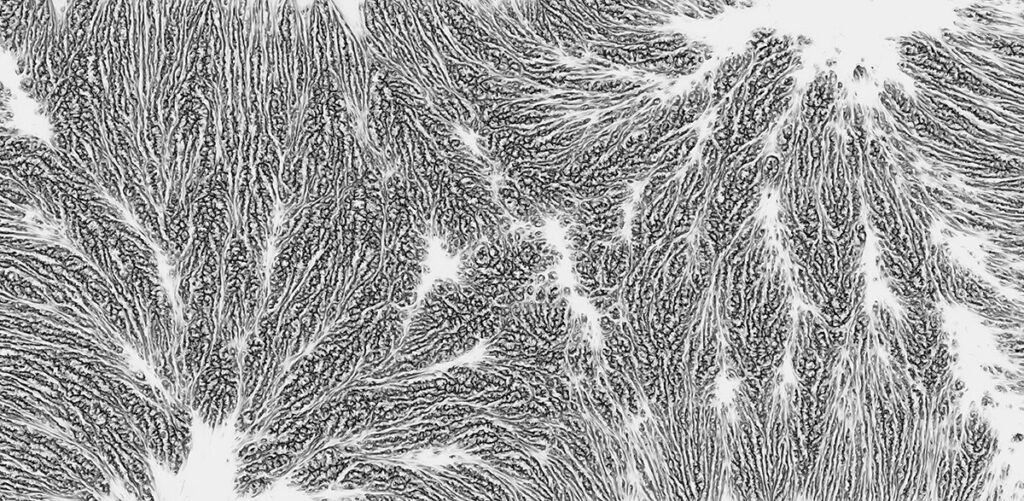
2D-Splitting is a rule of polyline growth and division to fill up flat or unflat surface using circle packing to prevent self-intersection. It is a typical example for algorithm learners.

Due to the simplicity of computing 2D, it’s easy to find examples on pages of openprocessing and github

https://adrianton3.github.io/differential-growth/
Triangular-Splitting
Triangular-Splitting is a common rule of 3D Differential Growth – mainly by “Growth” of mesh edges(details will be illustrated in next chapter). During the process, owing to the huge amout of growth computation, traditional mesh type cannot serach for a specific edge efficiently. Generally we use Half Edge Mesh for locating edges for splitting – a structure of mesh data with high efficiency. Albert Li introduced this structure in his article 网格学习笔记3——半边数据结构 , which said the pros and cons:
“Advantages:
the complexity of searching meshes is almost 0;
the complexity of editing meshes is almost 0;
Disadvantages:
Only manifold meshes can be expressed. (an edge can be counted as only two half-edges, the direction of half-edge cannot be defined if 3 faces are sharing one edge.)
The most interesting thing is that, the number of edges of this data structure is actually not limited (as long as the start and end of data is continuous and connected), in another word – it can express polygon mesh!”
Many examples of Triangular-Splitting – most of them are using half-edge to search for splitting edge efficiently. The process can be found in links provided in next chapter.
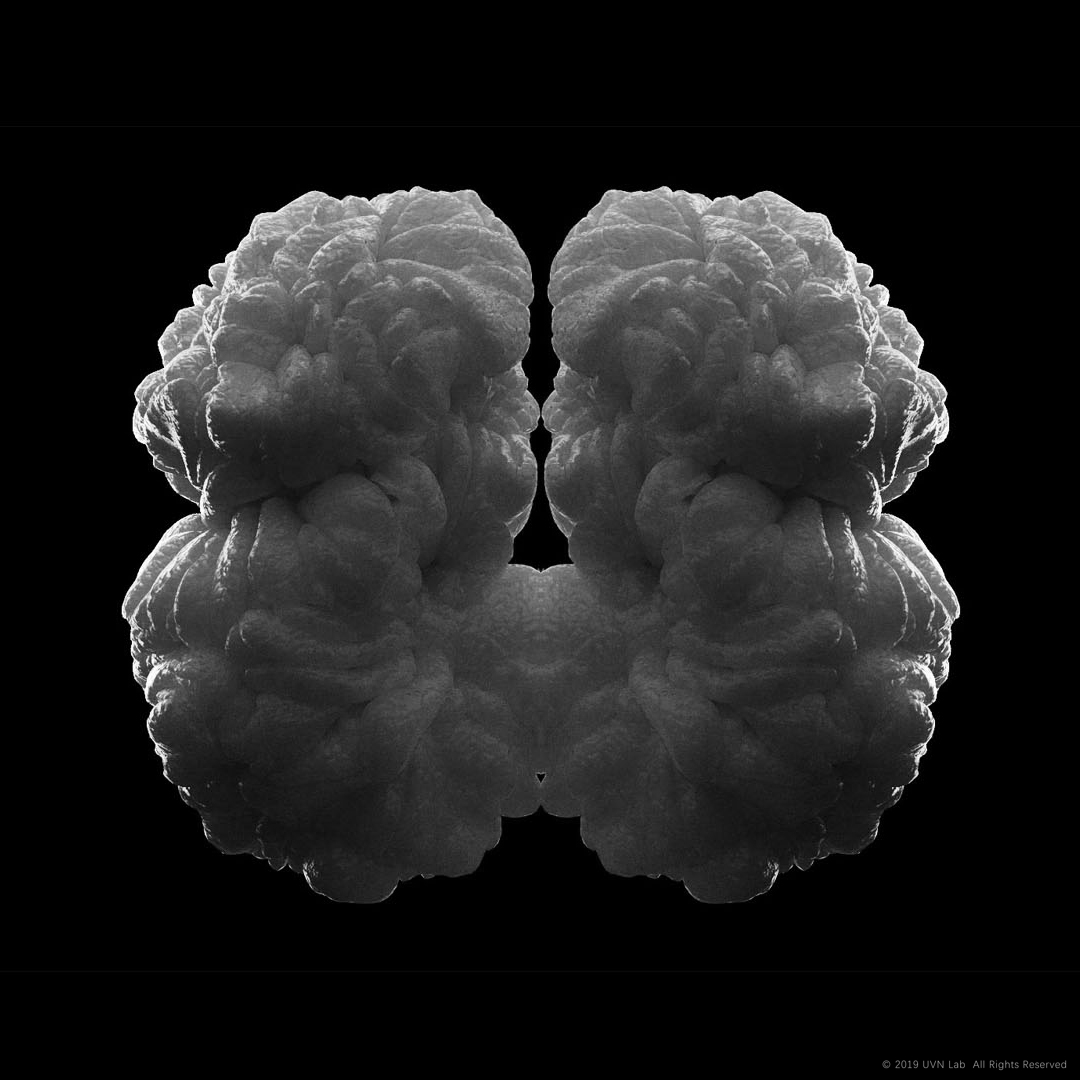
In 3D Differential Growth, open mesh and closed mesh will lead to drastically different form – former is more similar to pedals, and latter is closer to cellular venation and pattern of brain. But no matter how rule changes during the process, the space topology of geometry is fixed – closed keeps closed, open is still open and holes won’t change.
Image : https://grasshopper3d.com/
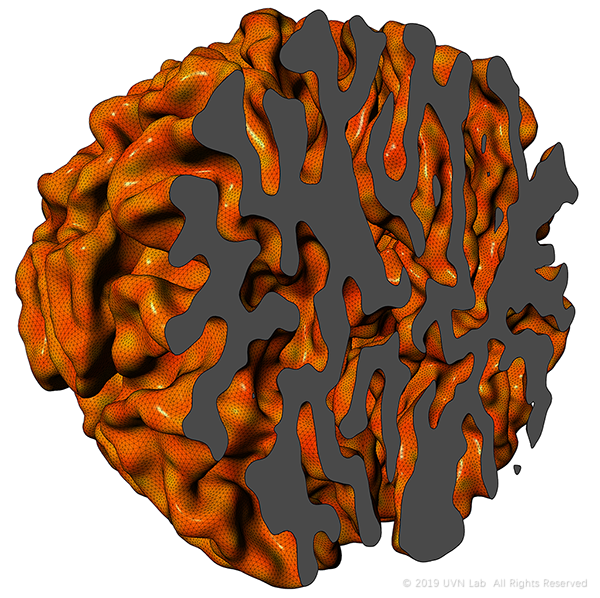
By cutting sections, it’s clear that the section of 3D Differential Growth is to tally same as 2D Growth.
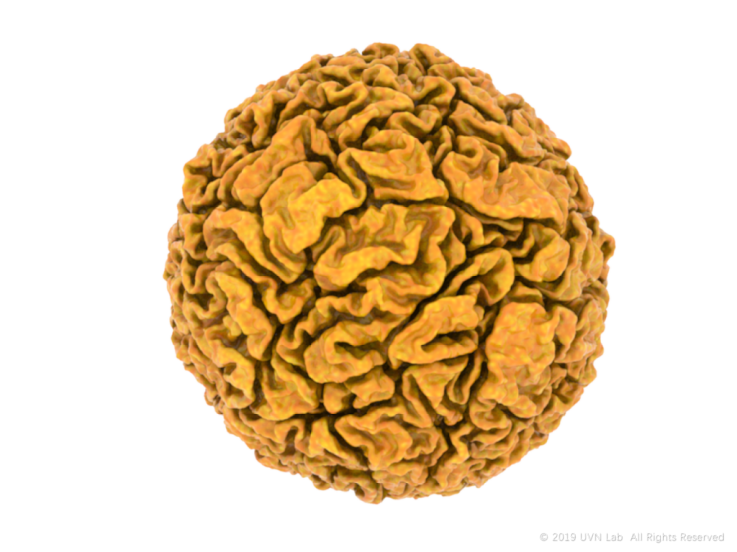
Hexagonal-Splitting
六边形规则相对三角细分复杂一点,也是一种常见的规则,通常选择六边形单元的中心对半切分,并消除掉其中一半的网格边,重新生成顶点并连接,这种方法不需要使用HalfEdge半边网格结构。虽然规则不完全相似,但生形过程与结果较为相近。
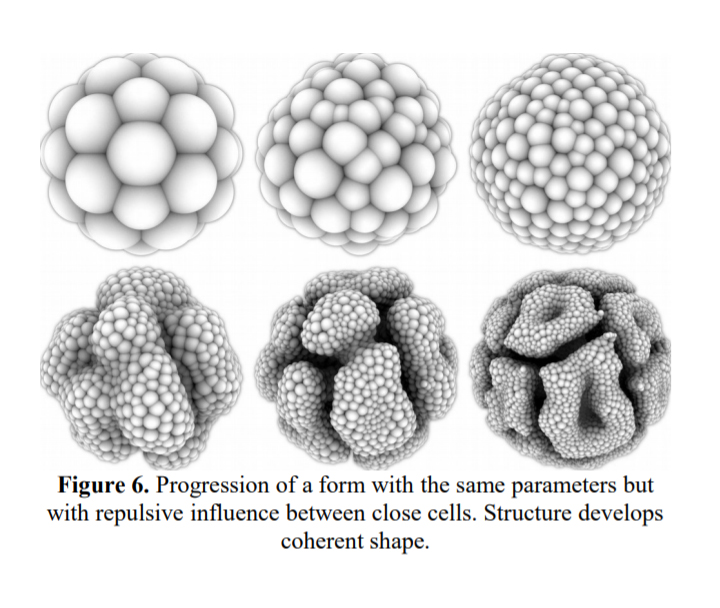
以下是Andy Lomas 的 Cellular Forms(https://www.andylomas.com/cellularForms.html)
He posted his article “Cellular Forms: an Artistic Exploration of Morphogenesis” on his personal webiste (http://www.andylomas.com/extra/andylomas_paper_cellular_forms_aisb50.pdf)
He concludes as below:
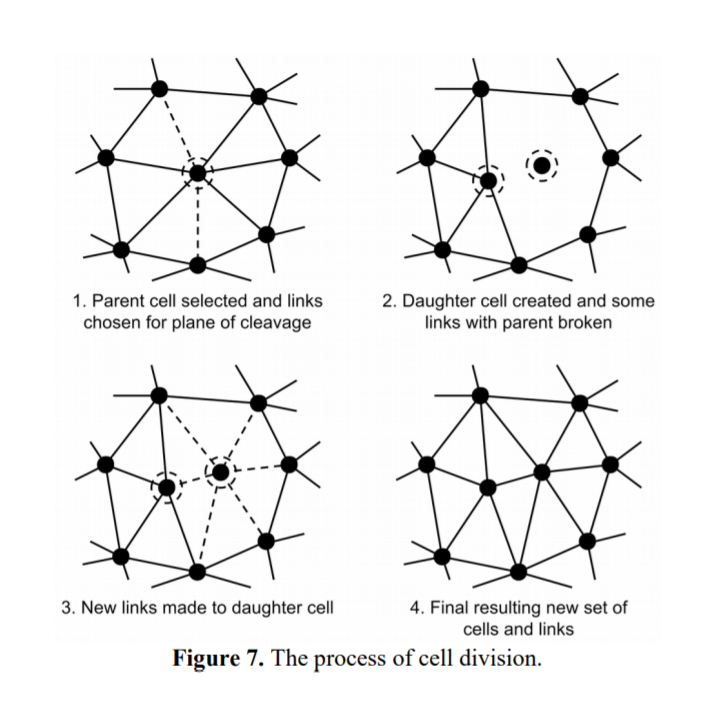
“Cellular Forms uses a simplified model of cellular growth to generate intricate sculptural shapes. Structures are created out of interconnected cells, with rules for the forces between cells, as well as rules for how cells accumulate internal nutrients. When the nutrient level in a cell exceeds a given threshold the cell splits into two, with both the parent and daughter cells reconnecting to their immediate neighbours. Many different complex organic structures are seen to arise from subtle variations of these rules, creating forms with strong reminiscences of plants, corals, internal organs and microorganisms.”
——Andy Lomas – Cellular Forms
His works are famous – Growth Forms,Hybrid Forms(Hybrid Forms combined different types of growth).In 2017, Karlsruhe Festival, he co-operated with ZAHA Studio to present a projection show of biological structures on building facades.
Except above, project by nervous system also implemented Hexagonal Splitting rule.( https://n-e-r-v-o-u-s.com/ )
Works below are “Growth Forms” by George W. Hart(http://www.georgehart.com/Growth/growth.html)
This series of work are usually referred in many researches.
Applications
Differential Growth is generally used in product design, jwellry and fashion, which is mainly by 3D printing. Pictures below are typical examples on pinterest – they are 3D printing jewllries by nervous system.
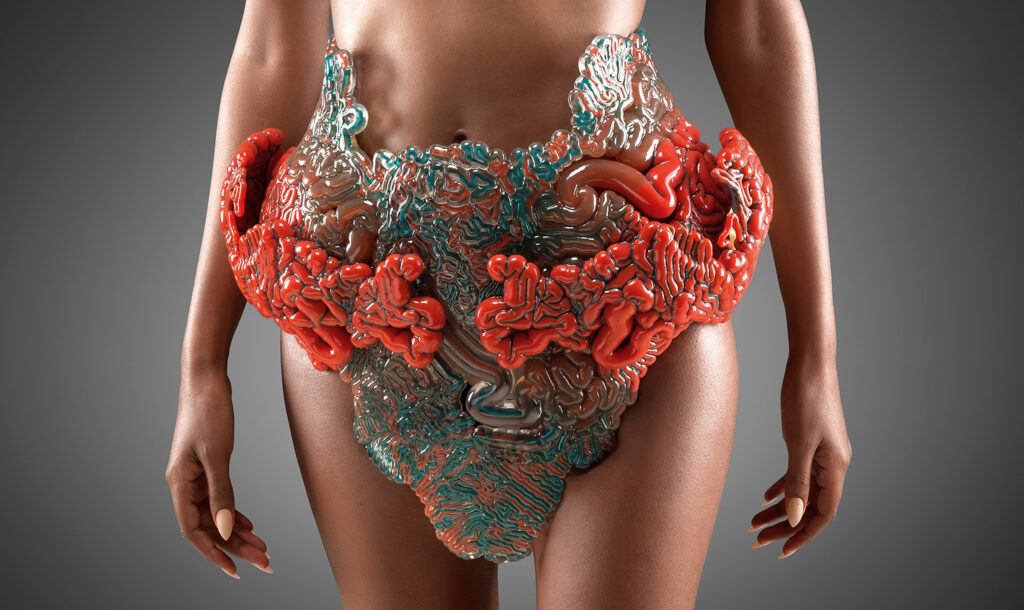
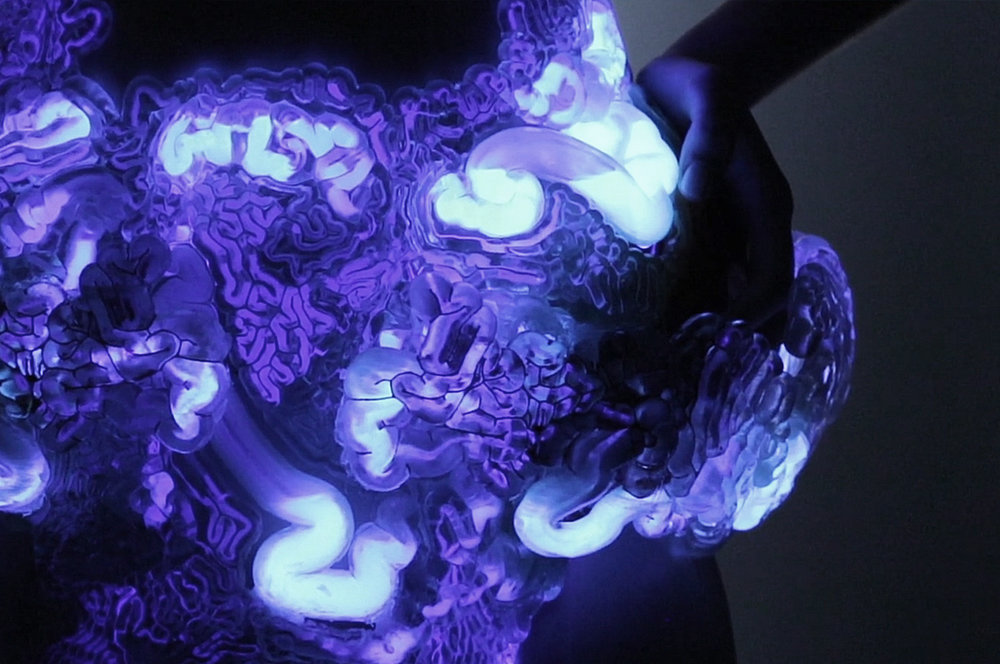
Many years ago, Neri Oxman from Media Lab leaded a group – Mediated Matter – which experimented several typical generative algorithm, and printed them out with bio-materials. Pictures below(2-1,2-2,2-3,2-4)all belongs to 2D Differential Growth,and picture 3-1,3-2,4-5,4-6 are 3D Differential Growth(except these, 1-1,1-2,4-3,4-4 are Reaction Diffusion)

Images below – Living Mushtari is a representative work of them – microbes are injected into cavities produced by biological form, to make a Self-circulating ecosystem.
Besides, Differential Growth is a common topic in digital-oriented schools. The picture below is “ClayFab” project by A.D programme in UCL Bartlett, which used the algorithm to generate path for 3D printing.
About few years ago, another project of them also used this method in 3D Growth.( https://b-pro.org/rc1-topoform )
3. Research
In 2017, I started to work on Differential Growth, and failed without knowing differences between it and other complex systems(such as DLA and Reaction Diffusion system)
Later accidently, an article “Curly Kale” by Daniel Piker(https://www.grasshopper3d.com/video/curly-kale-1) “Differential Growth in Curves” by Shridhar Mamidalaa(https://www.grasshopper3d.com/forum/topics/differential-growth-in-curves) largely inspired me – in which Daniel used Kangaroo for collision and smooth. Besides, David Bachman developed this project in a post “Growing Sphere” (https://www.grasshopper3d.com/group/kangaroo/forum/topics/kangaroo-inside-anemone-loop-to-change-geometry-during-simulation)
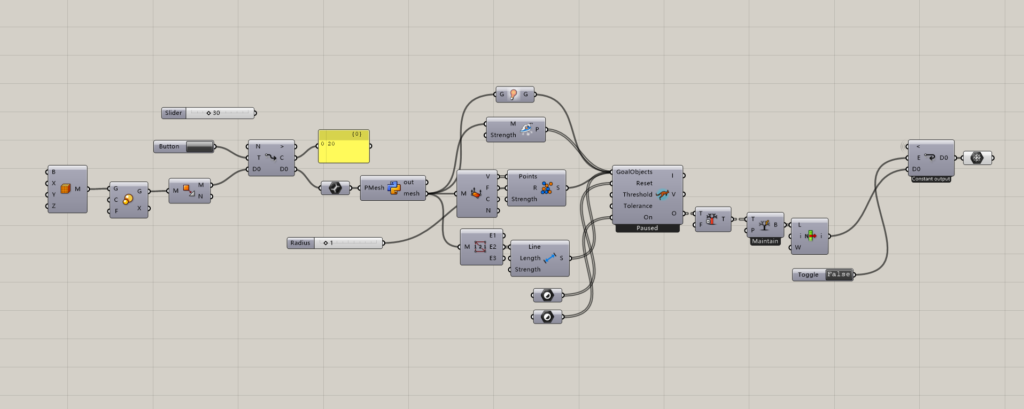
The process is:
1. Inside an Anemone loop, using PlanktonMesh to transform RhinoMesh to HalfEdgeMesh
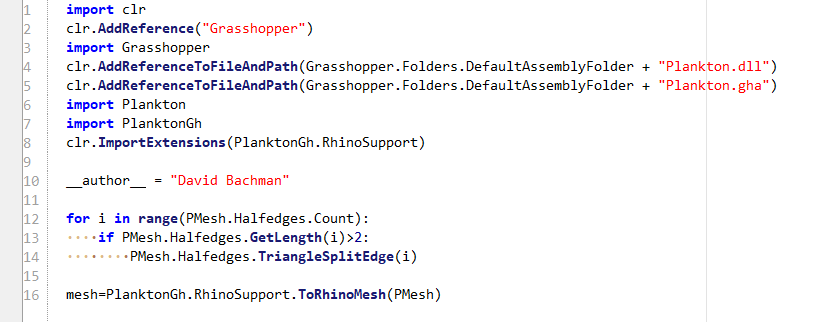
2. Split half-edges which exceeded a given length with GHpython module
3. Kangaroo 2.0 Solver:
A. Point-collision preventing self-intersection.
B. Force for growing edges.
C. Smooth sharp edges of mesh
4. Extract mesh, loop again
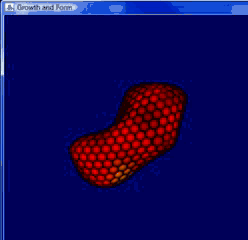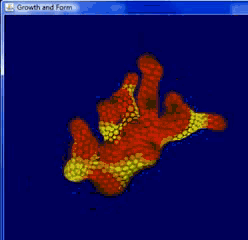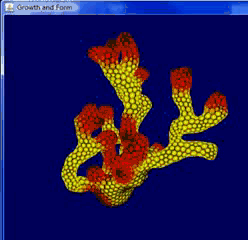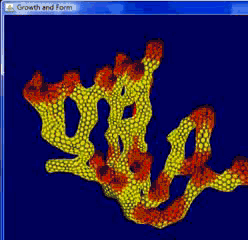
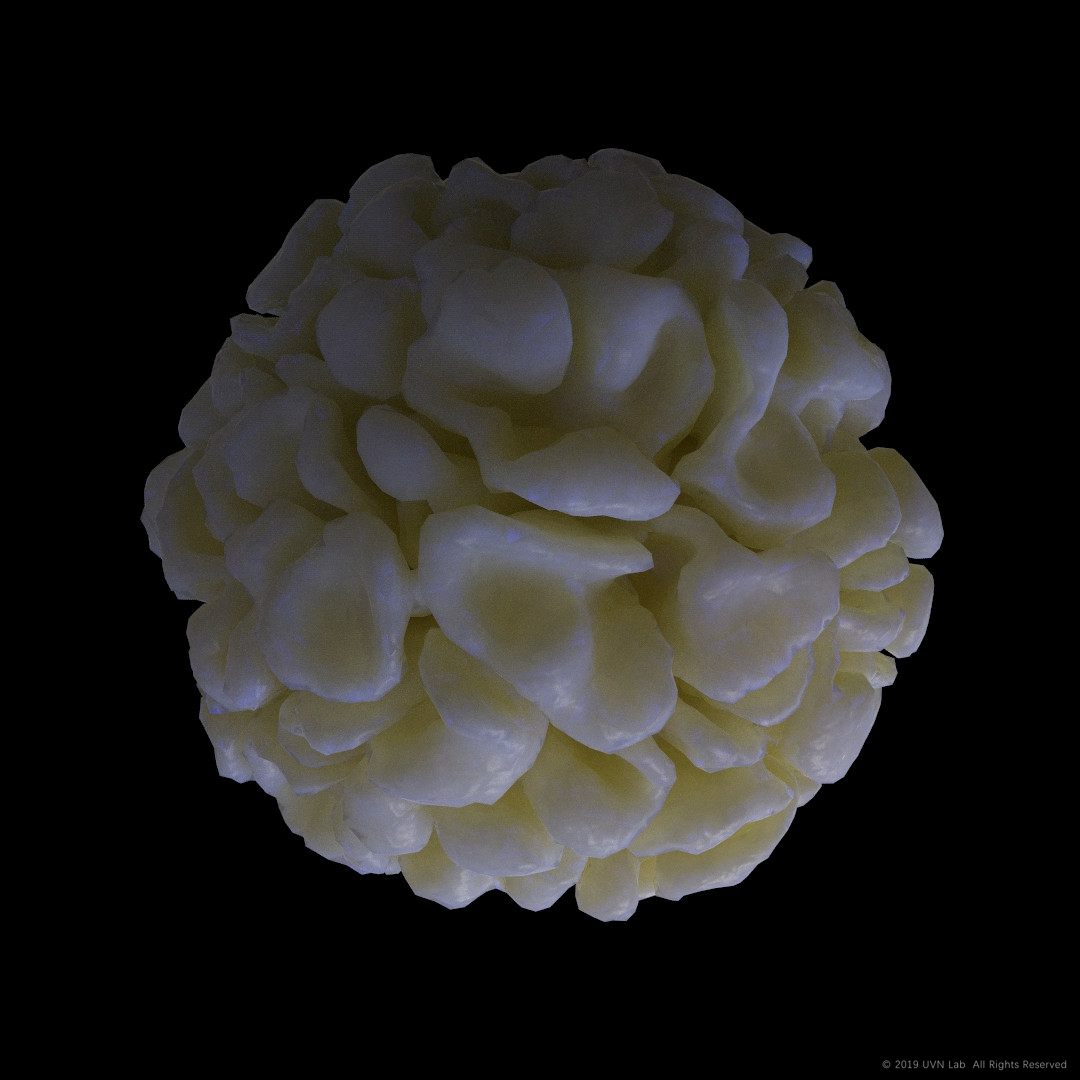
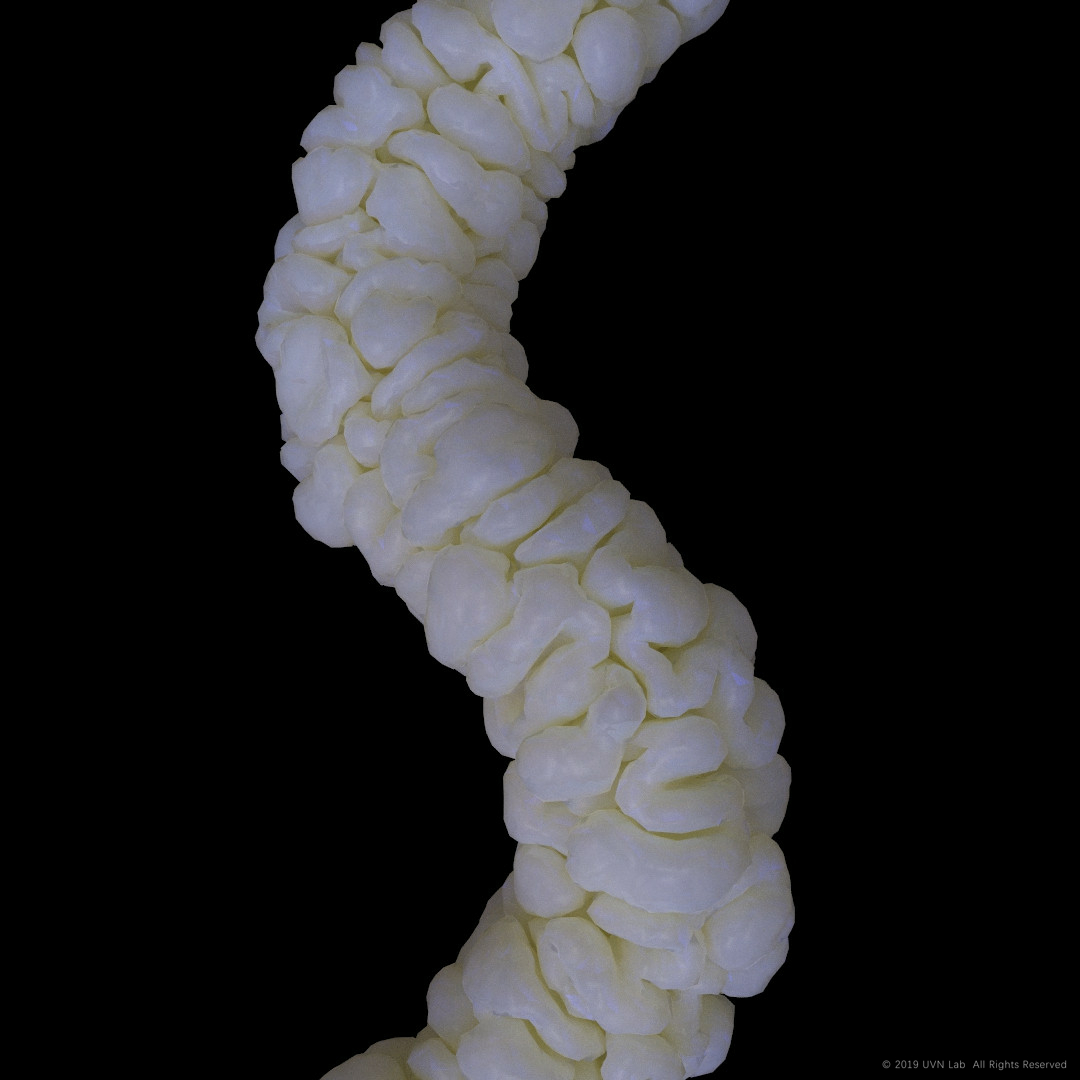
This method can produce “softer” shapre, but with much more mesh faces. (As two images below, are both less-differentiated but with millions of faces.)
When I was learning C# and in a tutorial by Long Nguyen I learned the pure C# method of Differential Growth(but the half-edge data should be used still.) And later I found a project by Vicente Soler on gh3D which perfectly made a differential growth without half-edge but a little bit slower than before (https://www.grasshopper3d.com/video/differential-growth).
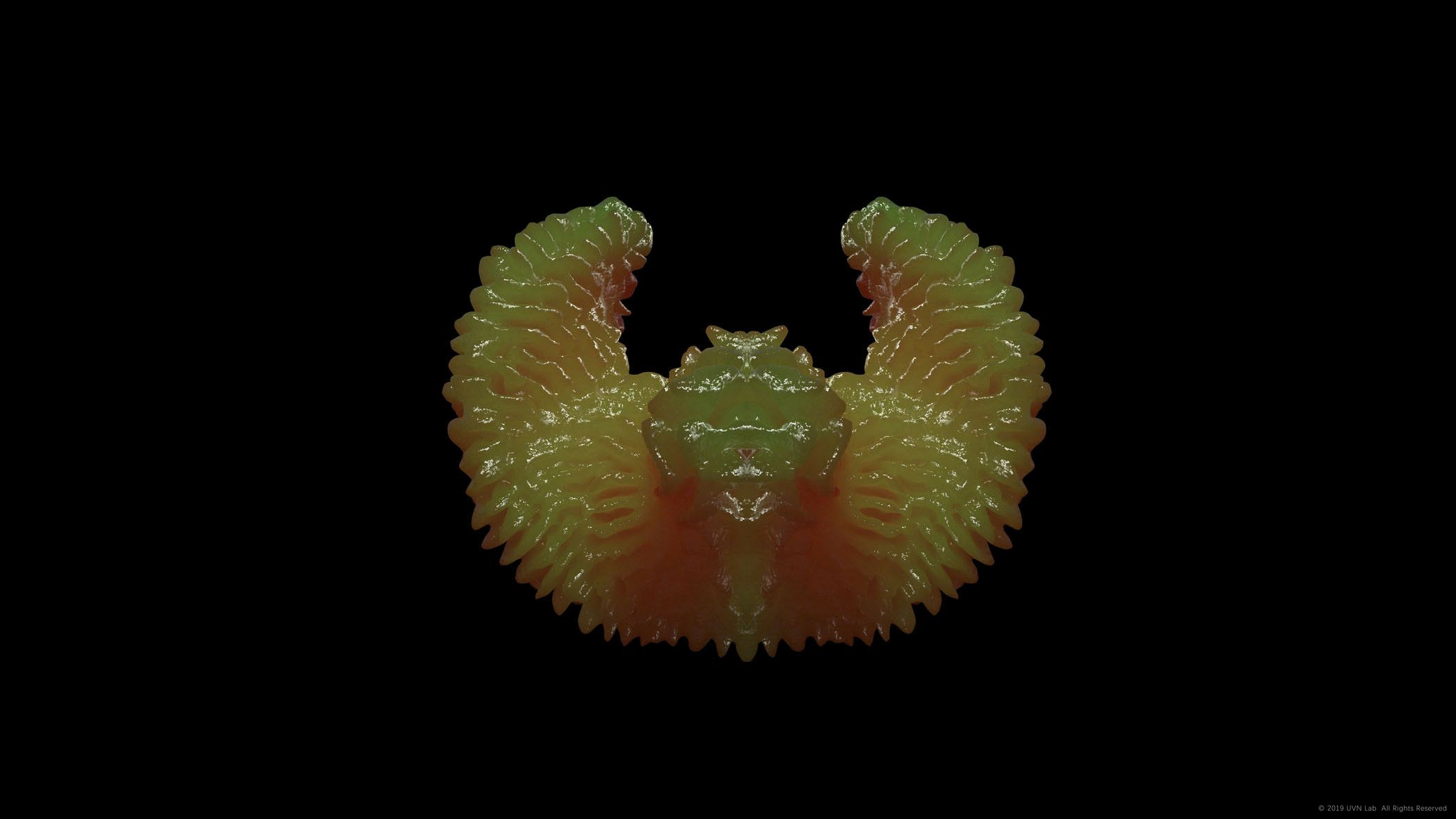
Owing to the imperfection of this rule in point-edge collision, which is based on distance between point and point, the growth form turns to be sharp and unaverage – but the generation can be much faster, and more complex form can be generated by fewer edges. (Picture below is an example by me, in which we can clearly identify the collision and division)





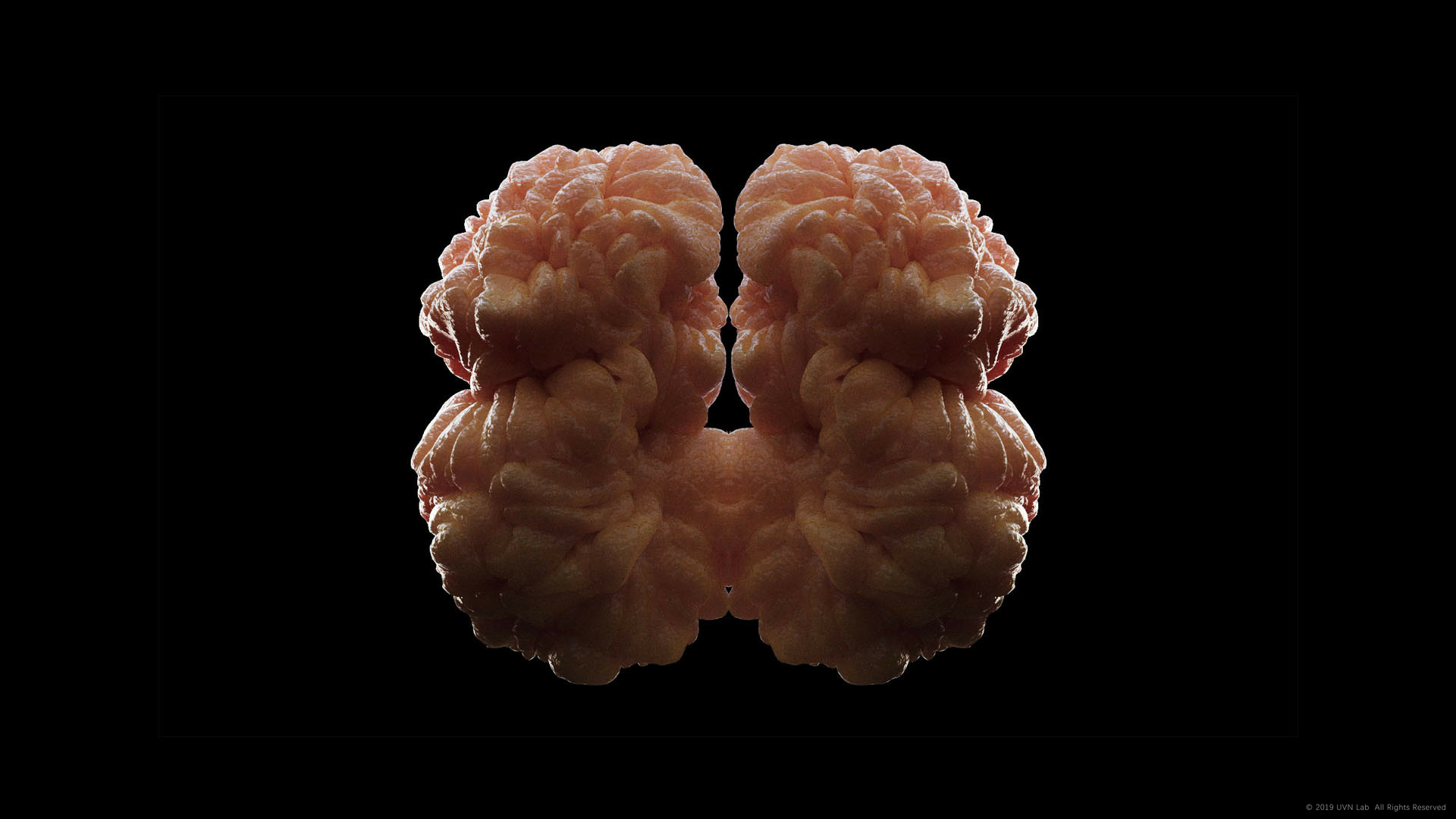
Though we discussed so much about Differential Growth, the results are almostly similar – especially as the iteration goes, the original feature will gradually blurs and become wrinky sphere in the end. In many examples we have in practice, the form iterates several times and generates a clear shape with features of the origin.
Technically, Differential Growth is too complex for a burbs platform such as Rhino, and it’s common in fields of animation, graphic and fx etc.(especially in platform of Maya、Houdini and C4D).
Differential Growth is just like all of other complex systems – it’s just a method of generating form, rather than copying any existing thing in nature. Many people asked me what I’m simulating in generative design – in my mind, the simulation is a simulation of design “structure” or “mechanism”, rather than its prototype. Just like plan, model or scanning, it’s just another way of abstraction and re-presentation, to transform the concept into new things. Researches on these rules are just a basis, to enhance the design. Just like what Andy Lomas mentioned in his project:
“The aim is to create structures emergently: exploring generic similarities between many different forms in nature rather than recreating any particular organism, in the process exploring universal archetypal forms that can come from growth processes rather than top-down externally engineered design.”
——Andy Lomas – Cellular Forms
Reference
[1] Jaap A. Kaandorp, Janet E. Kubler, The Algorithmic Beauty of Seaweeds, Sponges, and Corals, 2001
[2] https://www.grasshopper3d.com/forum/topics/differential-growth-in-curves
[3] Andy Lomas, https://www.andylomas.com/cellularForms.html
[4] https://n-e-r-v-o-u-s.com/projects/sets/floraform/
[5] http://www.georgehart.com/Growth/growth.html
[6] https://n-e-r-v-o-u-s.com/projects/albums/floraform-sculptures/
[7] https://deskriptiv.com/wanderers/
[8] UCL Bartlett, https://b-pro.org/rc5-clayfab
[9] UCL Bartlett, https://b-pro.org/rc1-topoform
[10] https://www.grasshopper3d.com/video/curly-kale-1
[11] https://icd.uni-stuttgart.de/?p=22773
[12] https://www.grasshopper3d.com/video/differential-growth
[13] Andy Lomas, Cellular Forms: an Artistic Exploration of Morphogenesis, 2014