前言
大概在2016年上半年,央美建院的一次内部工作坊当中,Chritoph Klemmt展现了他的Cell Based Venation Systems以及Andy Lomas,Deskriptiv 所做的一系列研究,从那时起我便被算法生形以及自组织的复杂形式所吸引,而Differential Growth这一经典模型对我来说更是启蒙性的,促使我后来展开了对其的深入研究,并探索了Reaction Diffusion,Multi Agent等等多种复杂系统,最后也启发我对“基础行为自组织系统”的实验。目前在中文网站上几乎没有相关资料,国外的资料也多属于医学或生物学领域。本期我就简单写一写关于Differential Growth的一些经典案例。
#1 定义
在医学上对于Differential Growth给出的释义如下:
different rates of growth in associated tissues or structures; used especially in embryology when the differences in growth rates result in changing the original proportions or relations.
在统一的组织或结构当中不同的生长率,通常指胚胎学中因生长率不同导致原来成分的比率与关系发生变化
——Farlex Partner Medical Dictionary © Farlex 2012
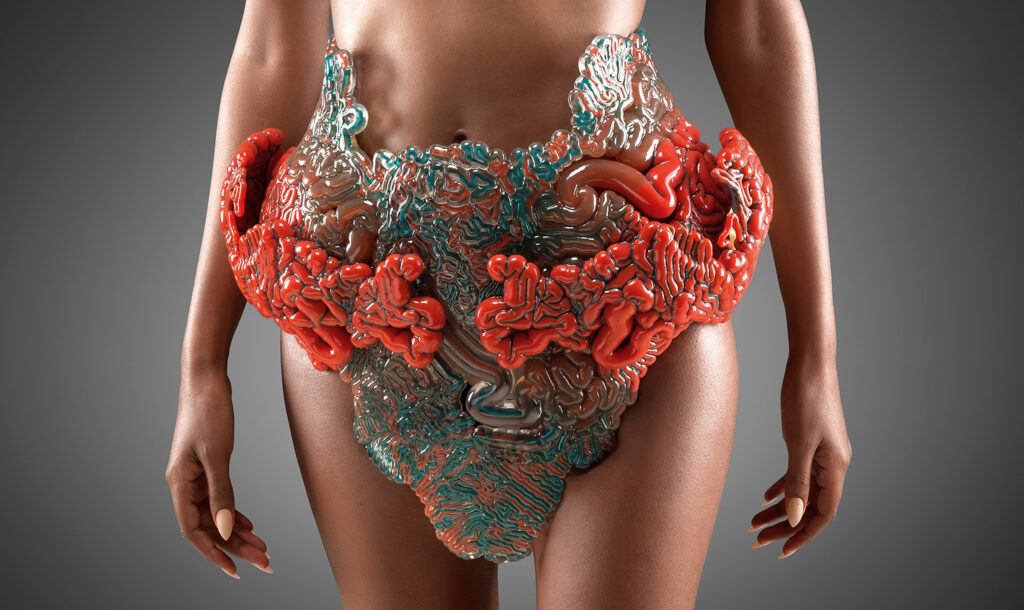
我们所说的Differential Growth属于是几何定义,和以上定义的“组织分化”有所区别,就和它的字面意思一样,我将其称为“差异化生长”——通过差异的扩增与分化,来发展出复杂的空间形态。它是一种在有限空间内通过褶皱增加结构利用率与复杂度的规则——大脑的褶皱用于容纳更多的神经元、肠道的弯曲与褶皱提高营养的吸收周期与吸收率、电脑芯片的数据量也取决于”褶皱“的复杂度。
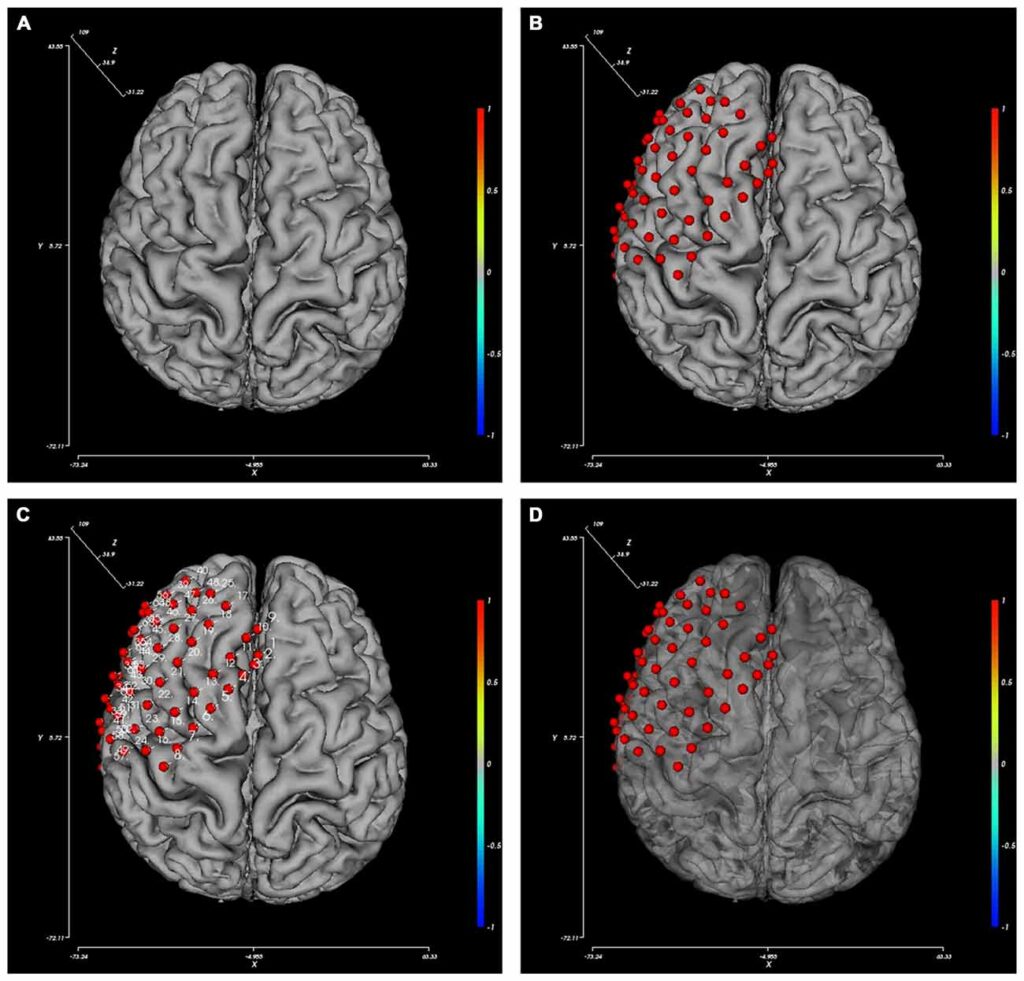
在我的观念中,Differential Growth也是一种行为间的动态平衡,生成的形式是动力间相互平衡的结果。
关于Differential Growth,有一本经典的书”The Algorithmic Beauty of Seaweeds, Sponges and Coral”,里面研究了若干海洋生物的形态,其中一部分珊瑚的生长模式就是标准的Differential Growth。


Differential Growth describes a surface that grows at different rates in different locations. Biological systems can create complex forms from the interaction of physical properties of a surface and simple controls of growth rates over time.
差异化生长描述了几何表面按不同位置不同生长率进行生长的模式。这一生物系统能随着时间的推移,通过几何体的物理属性相互作用以及简单的生长速率控制来产生复杂的形式。
——Nervous System
Differential Growth当中常常提到营养”nutrition“的要素(Andy Lomas以及上文等等都使用这一表述),它是一种生长率的权重,但这种权重并非是人为赋予或是来自另一套规则,而是几何体的自身属性——”营养“所指的其实是几何体的表面曲率,也就是Differential所指的”差异“,在其生形过程中不难发现,它始终遵循扩大曲率差异的规律,凹陷发展为沟壑,微凸发展为树状的组织,细微的差异会在数次迭代之后相差甚远。

#2 历史案例
Differential Growth的变体大概有三种:2D曲线细分,三角网格细分,六边形细分。在此处我们主要讨论的是3D细分,2D就不做赘述。
2D曲线细分
是大部分研究者的一项必修课,即通过多段线的生长与细分来填充平面或者非平坦表面,同时通过circle packing来保证碰撞体积,线段不会交叉。

由于2D计算量比较小,在openprocessing,github等网站均有网页版小程序

https://adrianton3.github.io/differential-growth/
三角网格细分
常见的3D生长规则,主要通过网格边的生长来完成面积扩增,同时通过网格边的细分来完成增殖,具体的原理将在下一章节讲到。在生长的过程中,由于数据量庞大,传统网格结构无法有效快速定位细分边,所以在计算过程中通常使用HalfEdge半边网格来对细分边进行定位——它是一种高效的网格结构,详情可以参考李至大神的文章 网格学习笔记3——半边数据结构,里面提到半边结构相对于传统网格的优势与劣势:
“优点:
所有网格查询操作的复杂度几乎为0;
所有网格编辑操作的复杂度几乎为0;
缺点:
只能表达流行网格。(因为一条边只能分成两个方向相反的半边,如果有三张面共边的情况,那么那条边的半边方向无法判定)
再给大家说一件非常有意思的事,仔细想一下的话,大家会发现这种数据结构,它的边数其实是没有限制的(只要保证边首尾相接,数据关系是非常清晰的),也就是说!它能表达多边形网格!”
在网上诸多三角细分的案例中,几乎都有使用半边数据结构来快速索引需要细分的网格边,具体原理可以参考下文链接当中的教程网址。
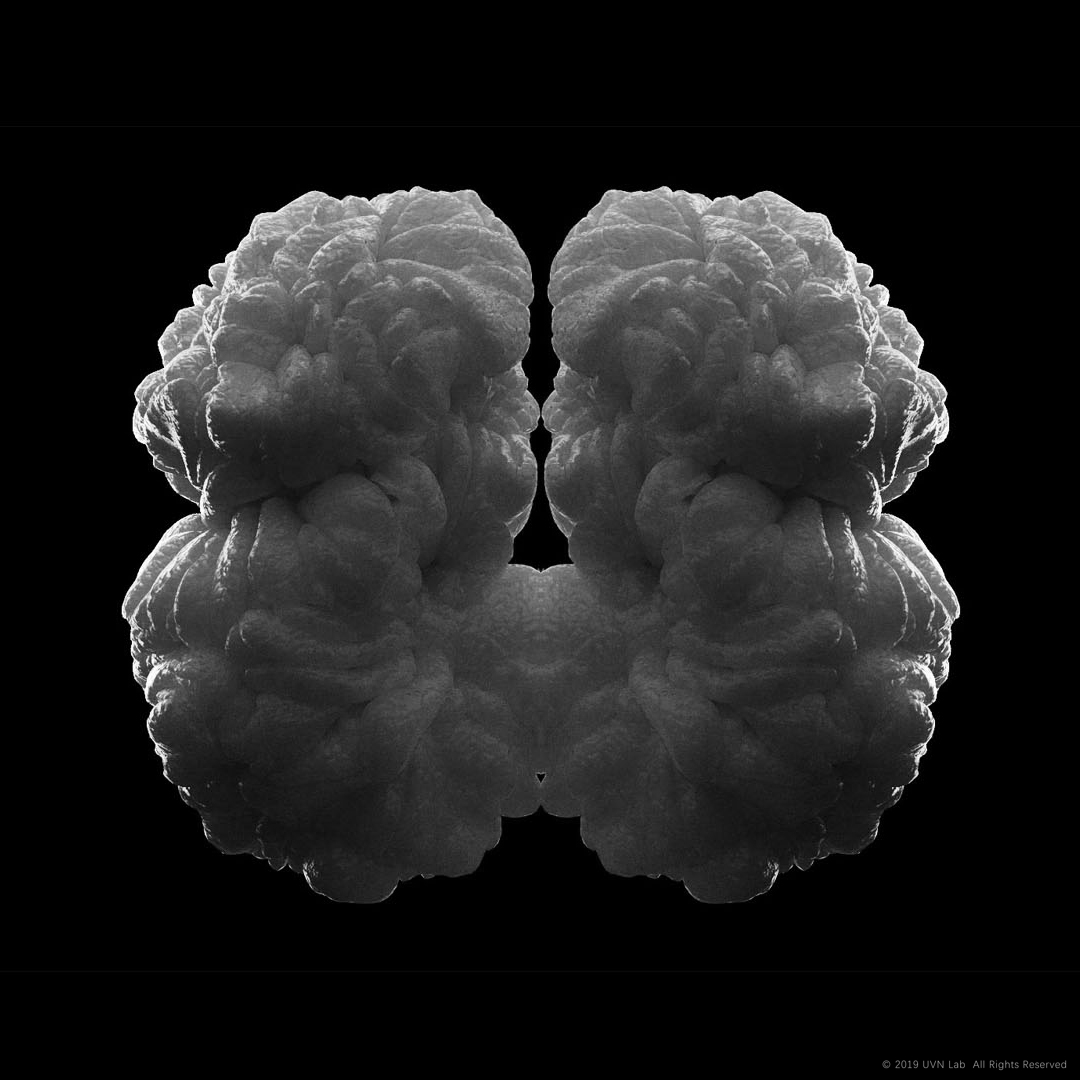
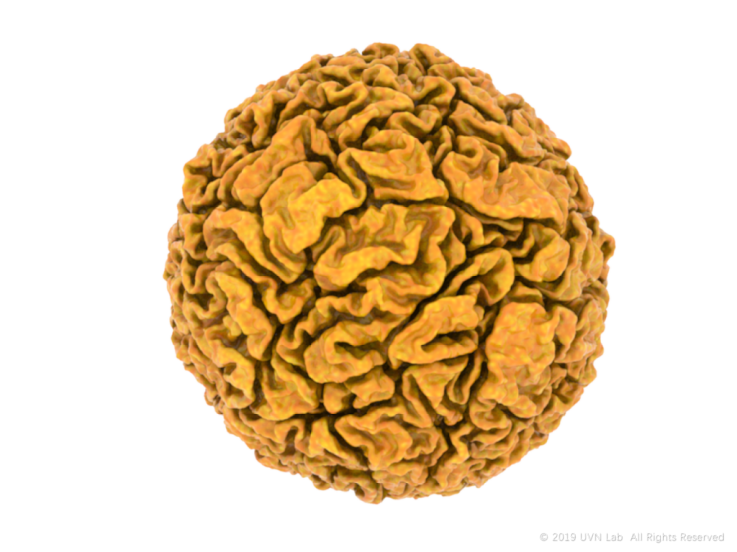
在3D Differential Growth当中,开放网格和封闭网格会生成两种截然不同的形式,前者更接近花瓣、木耳、菌类,后者则更接近细胞分裂或大脑纹路。不过,在Differential Growth的整个过程中,几何形体的空间拓扑关系都是不变的——封闭依旧是封闭,开放依旧是开放,孔洞位置依旧不变。
图片来自 : https://grasshopper3d.com/
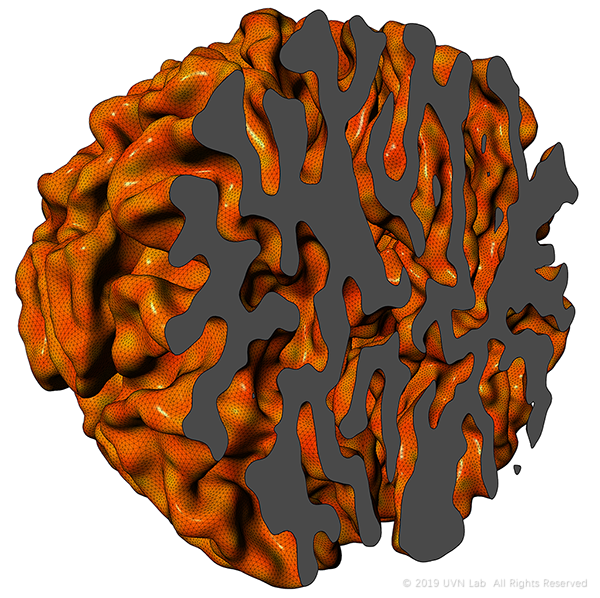
而通过切割,我们不难发现,3D Differential Growth的截面与2D规则的形态是完全一致的。
六边形细分规则
六边形规则相对三角细分复杂一点,也是一种常见的规则,通常选择六边形单元的中心对半切分,并消除掉其中一半的网格边,重新生成顶点并连接,这种方法不需要使用HalfEdge半边网格结构。虽然规则不完全相似,但生形过程与结果较为相近。
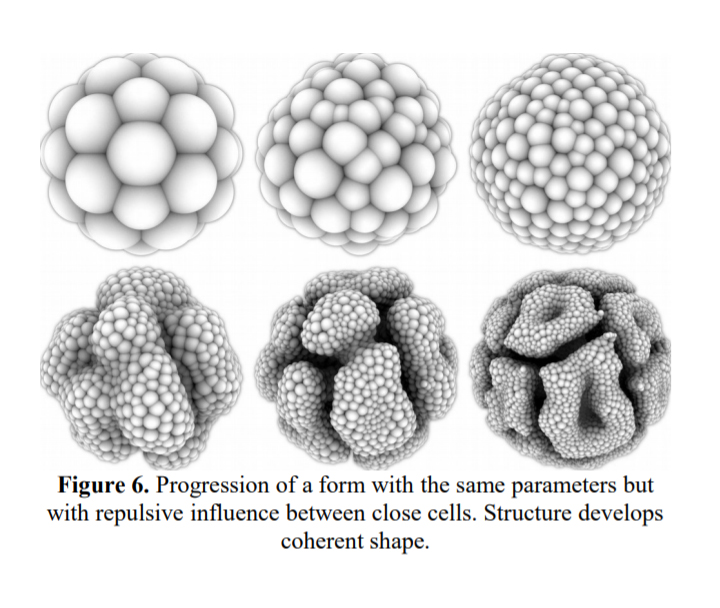
以下是Andy Lomas 的 Cellular Forms(https://www.andylomas.com/cellularForms.html)
他在个人网站上也贴出了自己的文章“Cellular Forms: an Artistic Exploration of Morphogenesis”(http://www.andylomas.com/extra/andylomas_paper_cellular_forms_aisb50.pdf)
他对自己的研究总结如下:
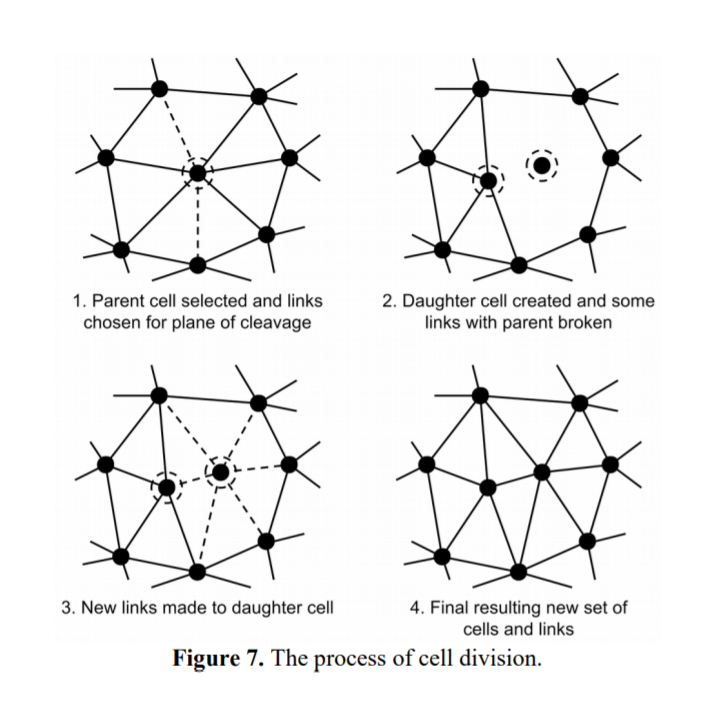
“Cellular Forms uses a simplified model of cellular growth to generate intricate sculptural shapes. Structures are created out of interconnected cells, with rules for the forces between cells, as well as rules for how cells accumulate internal nutrients. When the nutrient level in a cell exceeds a given threshold the cell splits into two, with both the parent and daughter cells reconnecting to their immediate neighbours. Many different complex organic structures are seen to arise from subtle variations of these rules, creating forms with strong reminiscences of plants, corals, internal organs and microorganisms.”
“Cellular Forms”项目使用了一种精简的细胞生长模型来生成错综复杂的、具有雕塑感的形态。结构由细胞间的力以及细胞的营养素累积规则控制,从相互连接的细胞单元中生成。当细胞的营养素超过了一个给定的阈值时,细胞一分为二,并且与周边的细胞重新构建连接。这些规则的细微改变都能产生许多不同的组织结构,产生的形式令人联想起植物、珊瑚、内脏以及微生物。“
——Andy Lomas – Cellular Forms
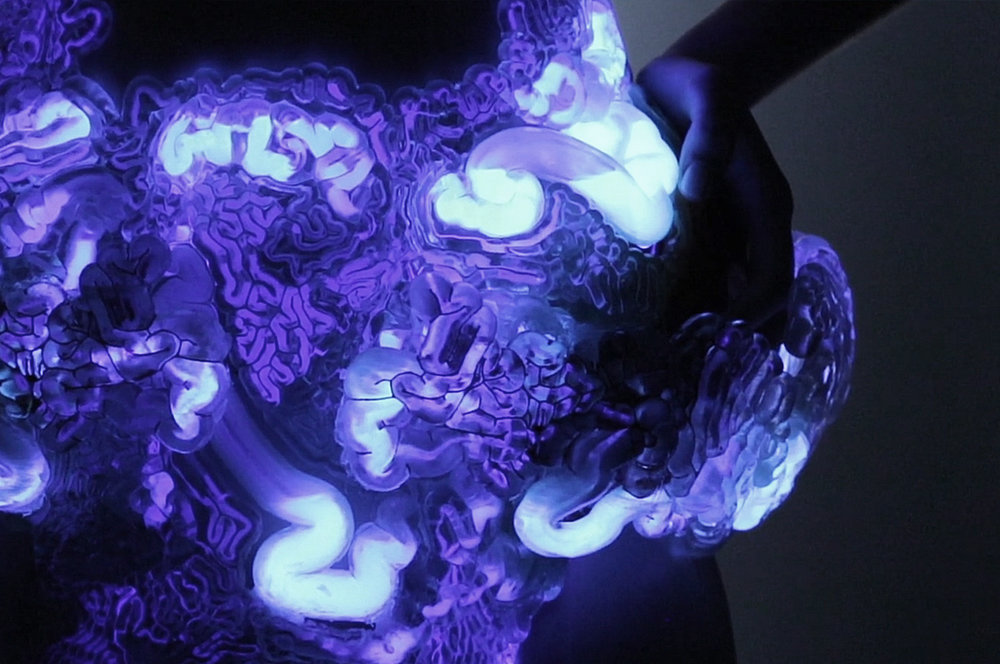
他的作品Growth Forms,Hybrid Forms等等都是广为人知的(其中Hybrid Forms更是融合了数种不同的生长类型),在2017年的Karlsruhe灯光艺术节上他也与ZAHA事务所合作了一场投影秀,将复杂的生物结构投影在建筑立面上。
除此之外,下图是nervous system的作品,也使用了六边形细分的规则( https://n-e-r-v-o-u-s.com/ )
以下是George W. Hart 在他的个人网站上所发布的”Growth Forms” (http://www.georgehart.com/Growth/growth.html)
这一系列研究也是经常被引用的经典
常见应用
关于Differential Growth的应用,比较常见的是产品、服装、首饰设计,而建造生产方式几乎都是通过3D打印。对于生形感兴趣的各位应该在pinterest上都见过如下几张图,它们就是上面提到的nervous system所做的3D打印首饰。
另外,多年前Media Lab当中由Neri Oxman带领的Mediated Matter就对多个生形算法进行过研究,并且通过生物材料对于这种有机形式进行过3D打印。下图中的2-1,2-2,2-3,2-4就是典型的平面Differential Growth,3-1,3-2,4-5,4-6则是3D Differential Growth(需要辨别的是1-1,1-2,4-3,4-4是Reaction Diffusion)

其中下图Living Mushtari是经典作品之一,在生成有机形式的同时,在空腔注入发光微生物,使得成品成为一个自循环的生态系统。
另外在国外数字化院校当中,它也是经典议题之一。下图是UCL Bartlett的AD所做的ClayFab作品,使用2D Differential Growth生成的路径来控制机械臂打印陶土
(不知道出于什么原因他们原本的网站w-o-n-d-e-r-l-a-b.com已经过期,详情可以到B.Pro的官网查看https://b-pro.org/rc5-clayfab)
另外在几年前其中一个小组的一件3D打印作品也使用了类似3D Differential Growth的网格细分。详情见 https://b-pro.org/rc1-topoform
3. 研究过程
在2016年下半年到2018上半年期间,我断断续续对Differential Growth进行了还原的尝试,最初在不了解它与其他生形系统的区别的情况下(比如用marching cube生成网格的粒子系统、DLA系统、3D Reaction Diffusion系统等等),用粒子等各种方法尝试还原失败了。
后来在2017年的时候,我偶然发现Kangaroo的开发者 Daniel Piker在gh3d官网上的一则老帖“Curly Kale” https://www.grasshopper3d.com/video/curly-kale-1,以及同时的另一篇来自Shridhar Mamidalaa的讨论帖当中”Differential Growth in Curves”(https://www.grasshopper3d.com/forum/topics/differential-growth-in-curves),Daniel使用Kangaroo完成了细分功能之外的计算(碰撞,平滑等等),后来David Bachman在帖子”Growing Sphere”当中对程序进行了优化,使其可以迭代并细分。(详情可以查看网址https://www.grasshopper3d.com/group/kangaroo/forum/topics/kangaroo-inside-anemone-loop-to-change-geometry-during-simulation)
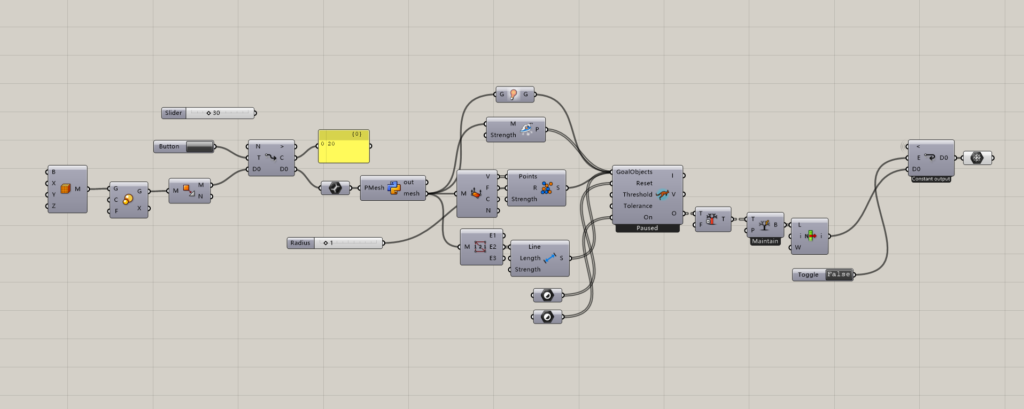
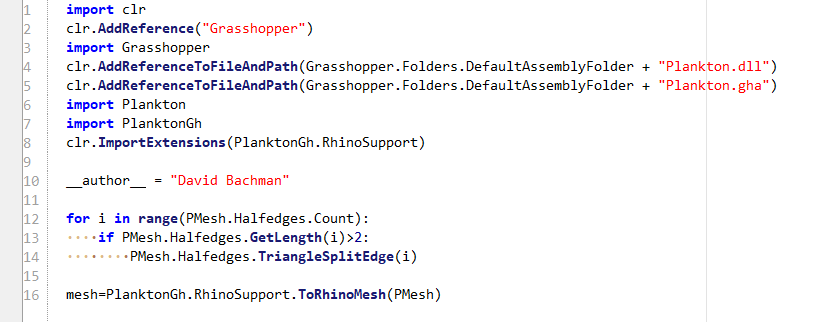
他所采用的做法是:
1. 通过在Anemone循环内,通过PlanktonMesh将RhinoMesh转化为HalfEdge网格
2. 再通过GHpython模块,对超过指定数值的半边进行中点细分
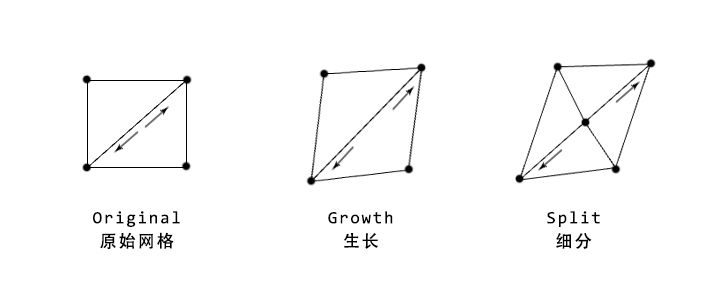
3. 连接Kangaroo 2.0的Solver,接入以下几个模块:
A.点碰撞,保证网格不出现自交
B.给每个网格边设定拉长的力
C.同时使用Smooth模块熨平Mesh的锋利边缘
4. 选出mesh,再次循环
在这一套逻辑下生成的形态更加圆润,但网格面数会陡增。下图两张图的模型虽然“分叉”不多,但面数均在几十万数量级。
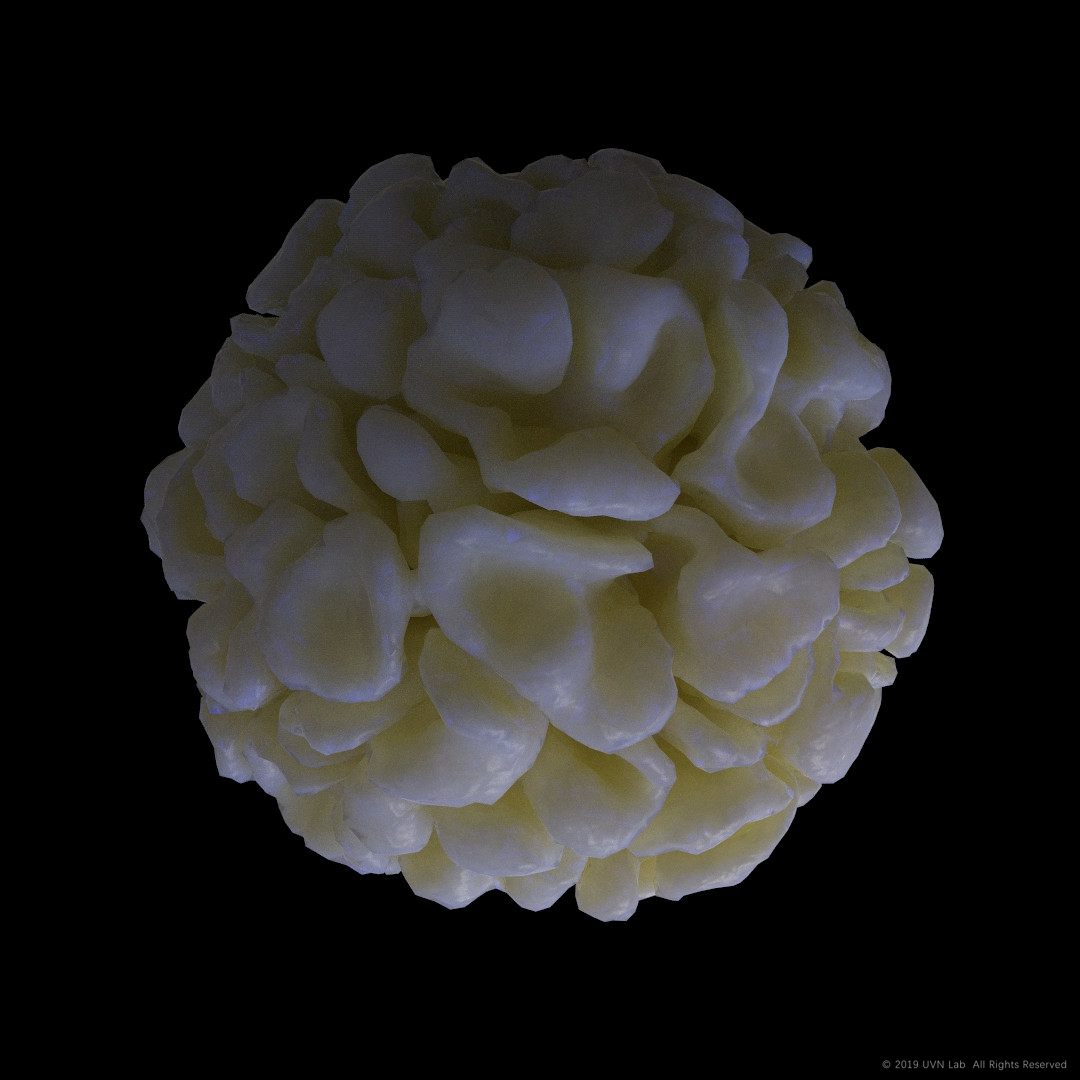
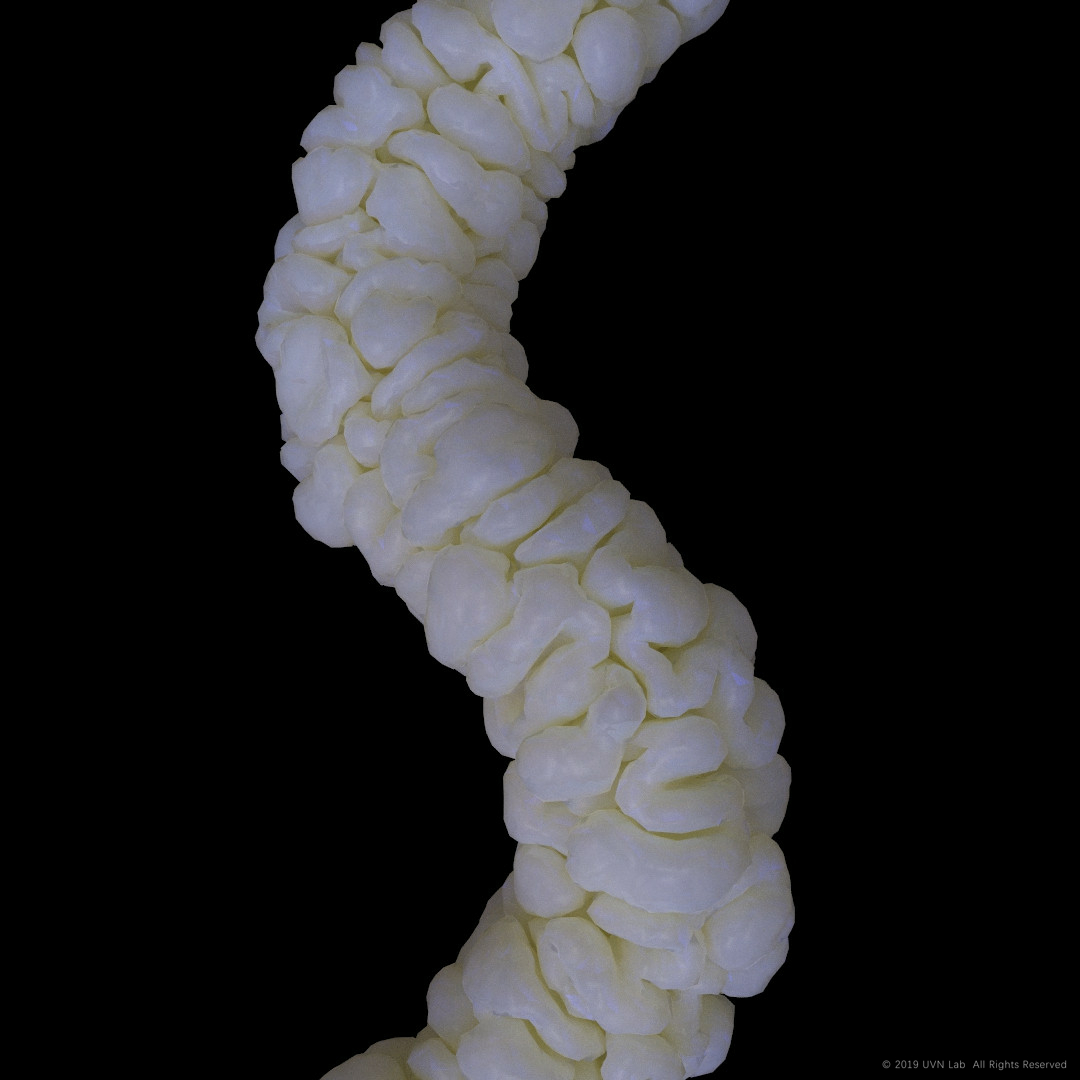
去年,在学习C#的阶段,网上四处找教程,在Long Nguyen的教程(这个教程主要关于GH C#以及gh开发,网址:https://icd.uni-stuttgart.de/?p=22773)当中就提到了Differential Growth的纯C#实现方法,不过,半边结构基础的数据结构依旧需要被引用。后来在gh3d论坛上,Vicente Soler的帖子就进行了C#编写的尝试,并且没有使用半边结构(https://www.grasshopper3d.com/video/differential-growth)不过整体效率略低于半边结构版本。
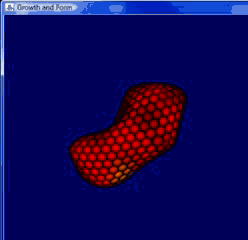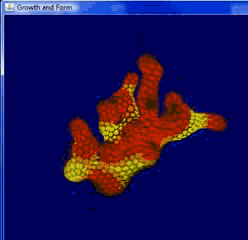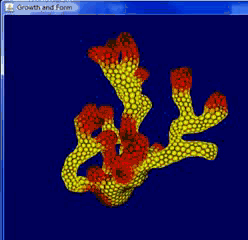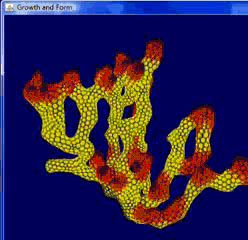
由于在这一套规则中,网格体积碰撞的规则基于点和点之间的直线距离,点与网格边的距离无法得到有效控制,最终生长的形式也显得较为锋利不够完美,但这一套逻辑生成的形态更加高效,用较少的面数即可达到更高的复杂度。以下均为我跟随教程还原的Differential Growth,网格动图可以清晰地看到点和点之间如何碰撞,边线如何细分。





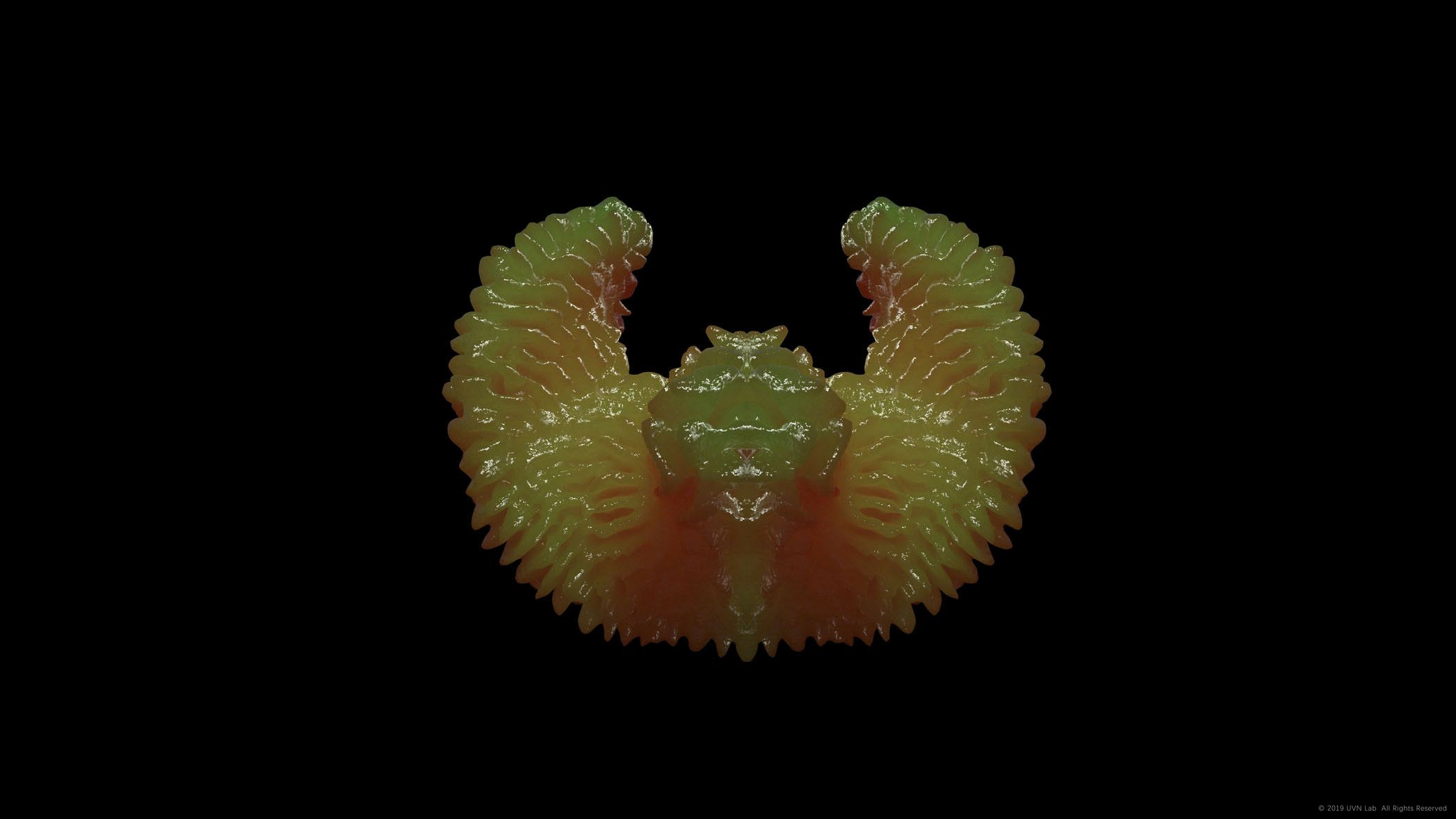
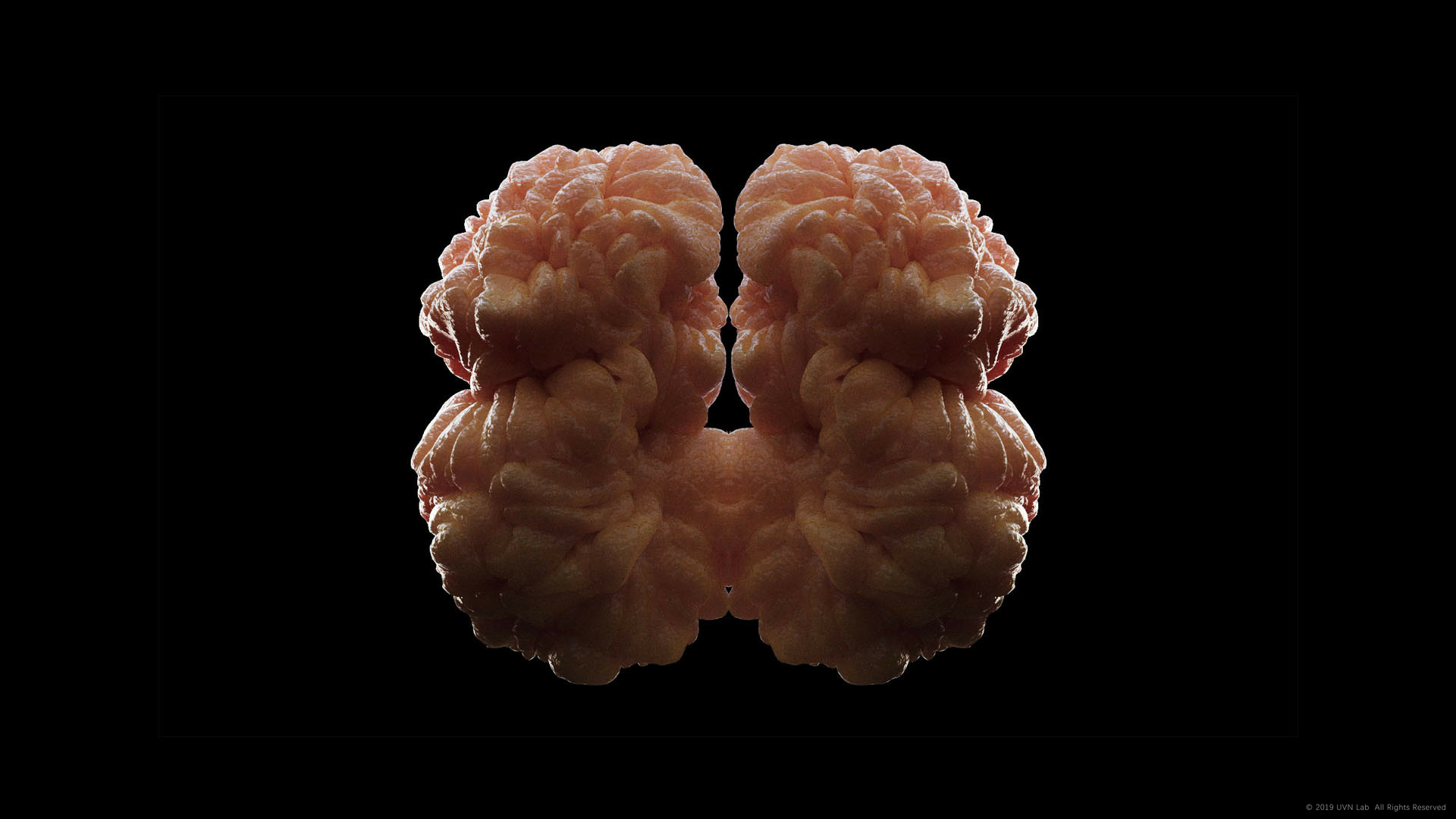
其实Differential Growth的结果都相对趋同,尤其随着迭代次数增加,最初的形态特征渐渐消失,最终都无外乎变成充满褶皱的球,所以在许多已有的案例当中,生形的迭代次数都不多,基本都保持了最初的大形。
从技术上来讲,Differential Growth对于Rhino这样一个nurbs软件来说做起来并不方便,而在动画、影视特效等等领域,这样的生成在Maya、Houdini、C4D当中则是非常常见。
从应用上来讲,Differential Growth和其他复杂系统一样,都是一种生成形态的方式,而非还原或者模拟任何一种自然界当中的原型。曾经有不少人对于生成设计提出疑问“模拟是为了什么呢”,我认为其实这种模拟,无论是哪种模型,都是指向设计架构的模拟,而不是模仿其原型。和图纸、模型、扫描一样——作为一种结构的再现与抽离,它既不是为了复刻某一种既有的原型,而是通过概念的转换生成新的事物。充分研究和提炼这些规则,也是为了设计而做的准备。Andy Lomas在他的项目介绍当中也说到:
“The aim is to create structures emergently: exploring generic similarities between many different forms in nature rather than recreating any particular organism, in the process exploring universal archetypal forms that can come from growth processes rather than top-down externally engineered design.”
“(这一项目)的目的在于用生成的方式来创造结构:在探索一种普适性的、能从自下而上的生长而非自上而下的设计中生成形式的过程中,从诸多不同自然形态当中寻找生成模式的相似性,而非重建还原某一种特定的生物组织。”
——Andy Lomas – Cellular Forms
参考
[1] Jaap A. Kaandorp, Janet E. Kubler, The Algorithmic Beauty of Seaweeds, Sponges, and Corals, 2001
[2] https://www.grasshopper3d.com/forum/topics/differential-growth-in-curves
[3] Andy Lomas, https://www.andylomas.com/cellularForms.html
[4] https://n-e-r-v-o-u-s.com/projects/sets/floraform/
[5] http://www.georgehart.com/Growth/growth.html
[6] https://n-e-r-v-o-u-s.com/projects/albums/floraform-sculptures/
[7] https://deskriptiv.com/wanderers/
[8] UCL Bartlett, https://b-pro.org/rc5-clayfab
[9] UCL Bartlett, https://b-pro.org/rc1-topoform
[10] https://www.grasshopper3d.com/video/curly-kale-1
[11] https://icd.uni-stuttgart.de/?p=22773
[12] https://www.grasshopper3d.com/video/differential-growth
[13] Andy Lomas, Cellular Forms: an Artistic Exploration of Morphogenesis, 2014