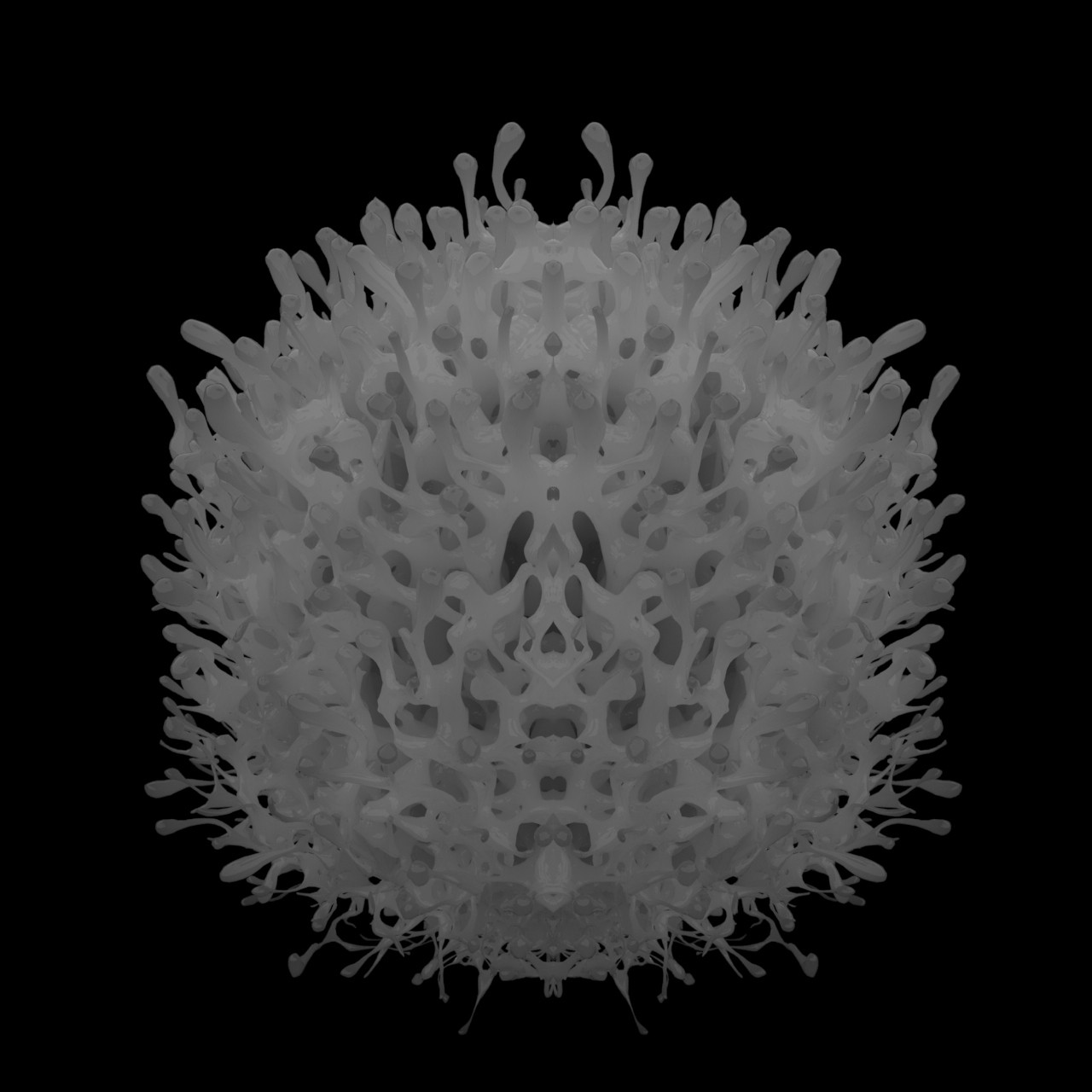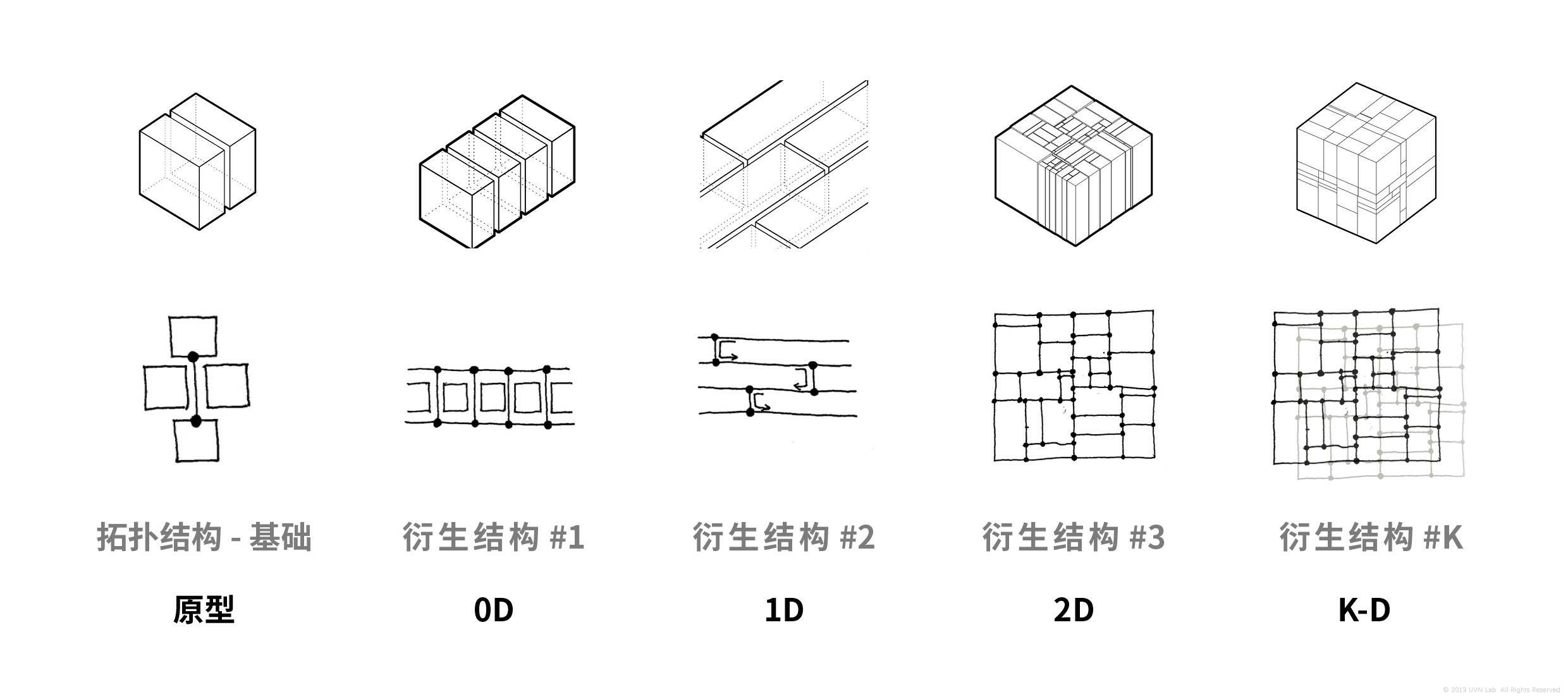
本期分享的是我近期一系列关于二叉树算法的简短研究(二叉树是一种经典的数据结构,常用于空间划分,数据搜索与图像处理)。出于本科毕设“夹缝+”的需求,我需要用可控的二叉空间划分法,来生成一套具有密度与层级变化的空间网格,进而展开设计。此次研究包含了多种控制方法的研究,也包括了经典的K-D Tree这一模型。
1. 简单二叉树
1. 给定划分范围
2. 计算区域的长宽比
3. 在区域的长轴上沿短轴方向划分
4. 将划分完的空间分别归入子层级的两个节点中(左0右1)
5. 回到第一步

2. 比率控制/ Ratio Based
第二阶段的研究纳入了比率的控制
即划分点在长轴区间的百分比
控制这一比率即控制划分的左右
整体的形式会根据左右的比值呈现不同的密度与形态
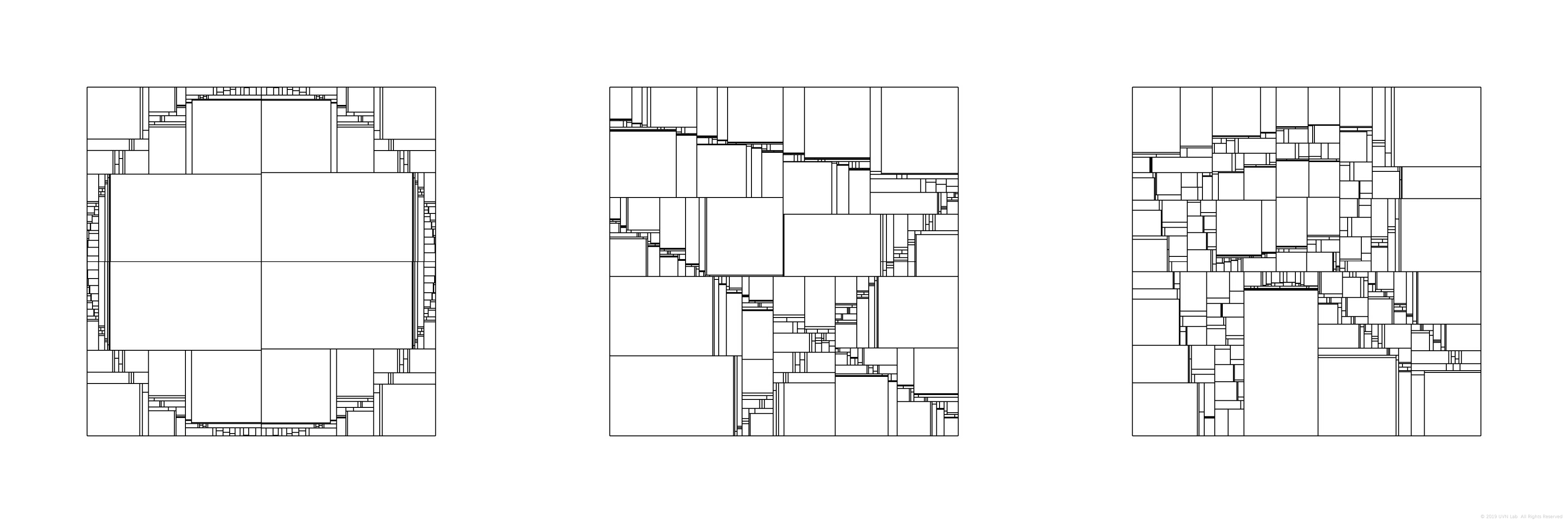
从标准正方形网格到K-D Tree
都是二叉树的一种分支

二叉划分点的偏移会产生复杂的网格系统
父级的偏移直接影响到子级

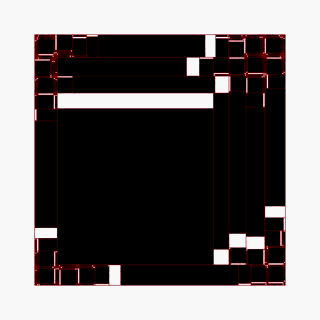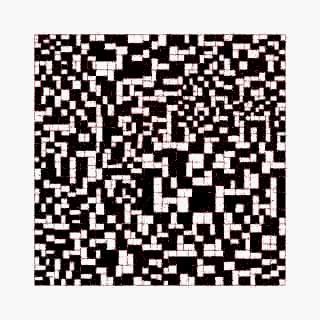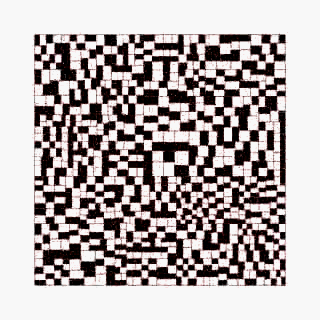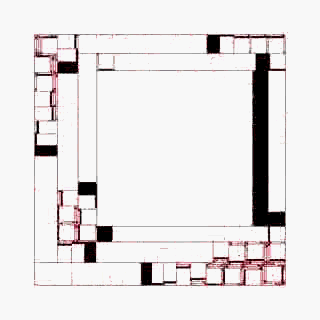
随着迭代的增加,微观层级上的差异逐渐在宏观层面上表现出丰富的变化,划分点的细微差异导致巨大的分化。




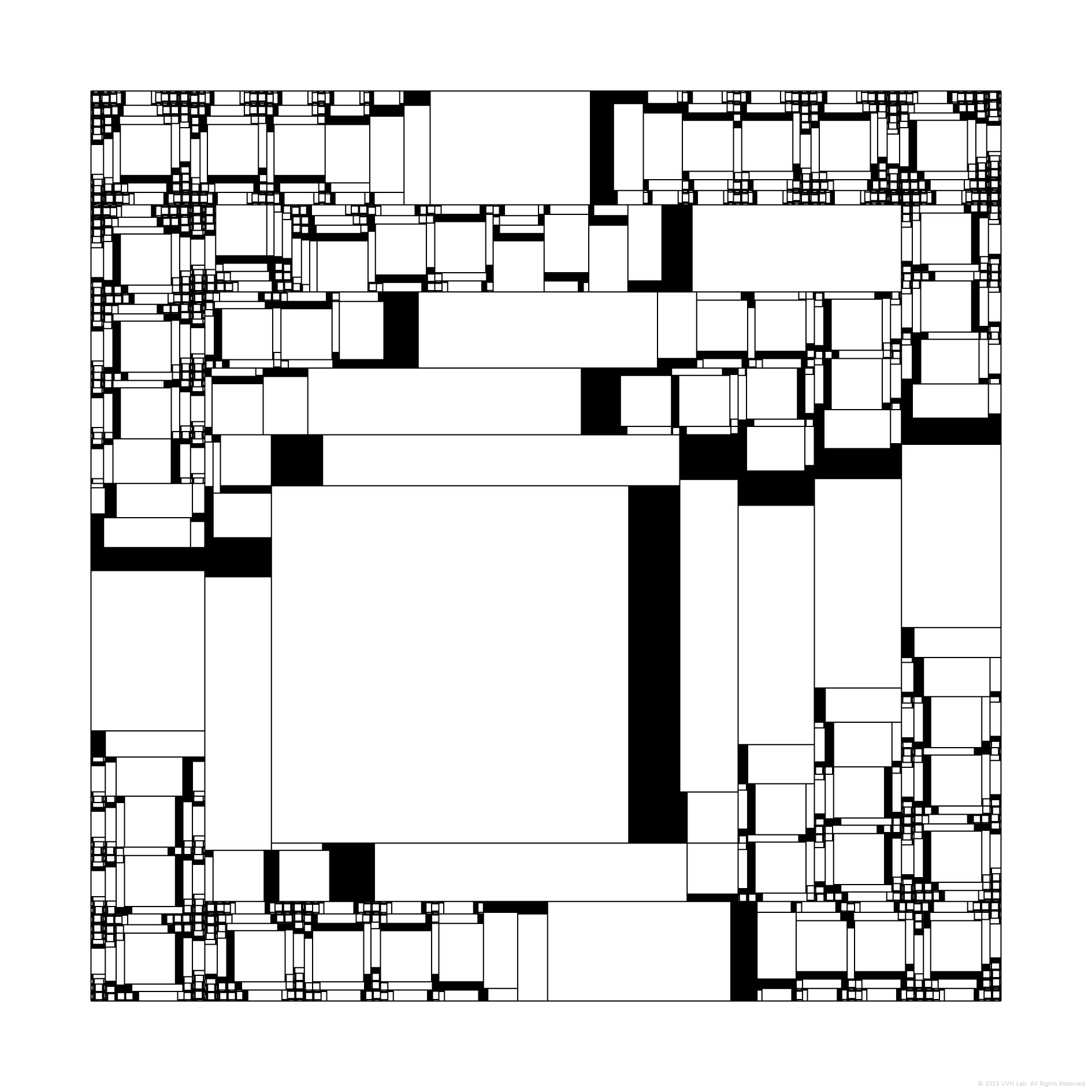
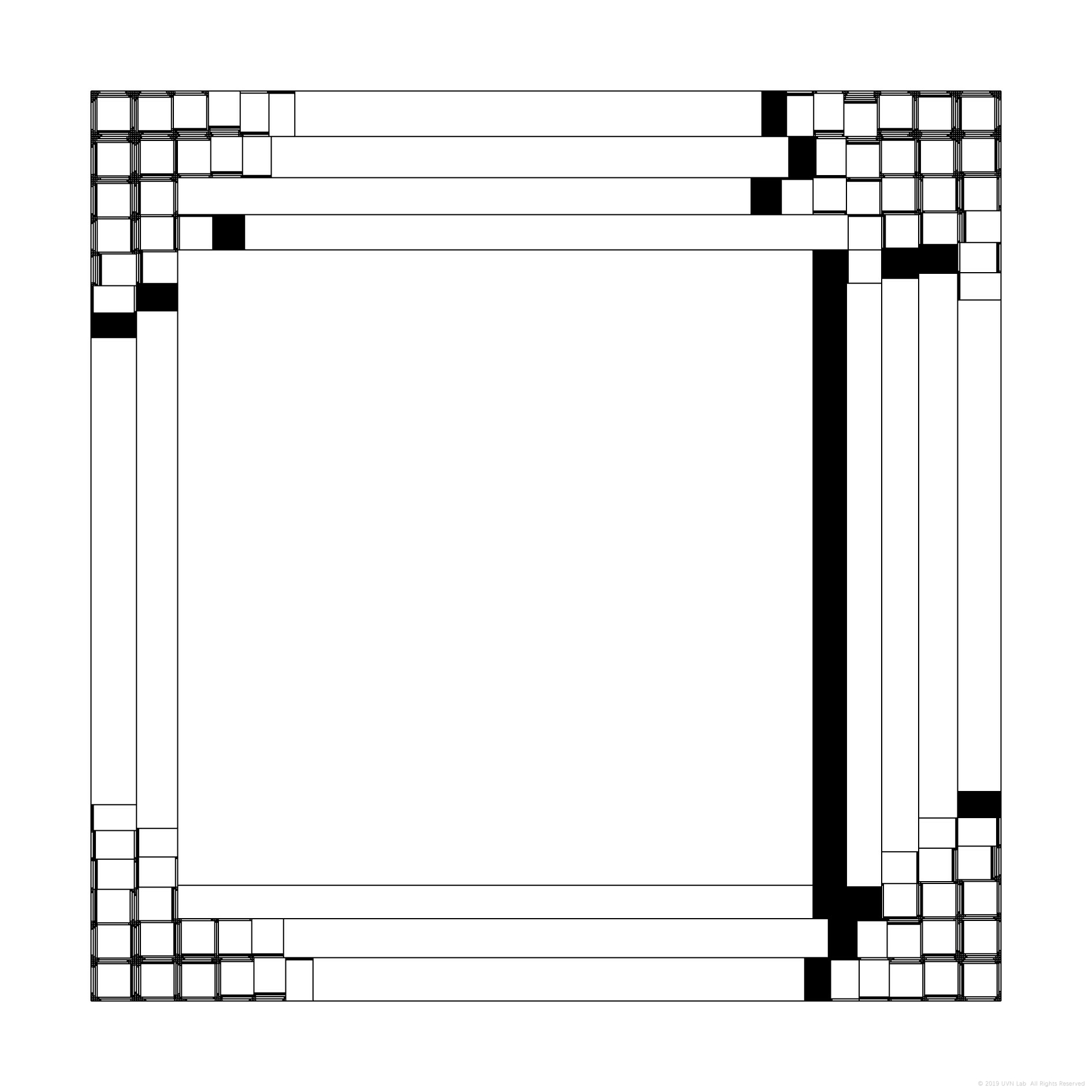

其中父级与子级之间恒定不变的数学关系使得各个层级之间具有高度相似性,偏移点向左或向右使得颜色的分布比例以离散的方式偏向一边,但在整个过程当中,二叉树的拓扑结构是不变的
ps:以上划分均在区域范围内按比值划分,假如长轴上的划分按照绝对数值进行,超出长轴范围的点将不会划分,二叉树将不是满二叉树。整个结构是不均匀的 —— 这样一来并非每一个父节点都将对应两个子节点,或是并非每一个父节点都有相同深度的子层级。
3. Gray-Value Based | 灰度控制
第三阶段的研究基于图像的灰度,每一次的划分都会根据区域内图像灰度采样,并计算出中值点,再沿短轴方向划分。
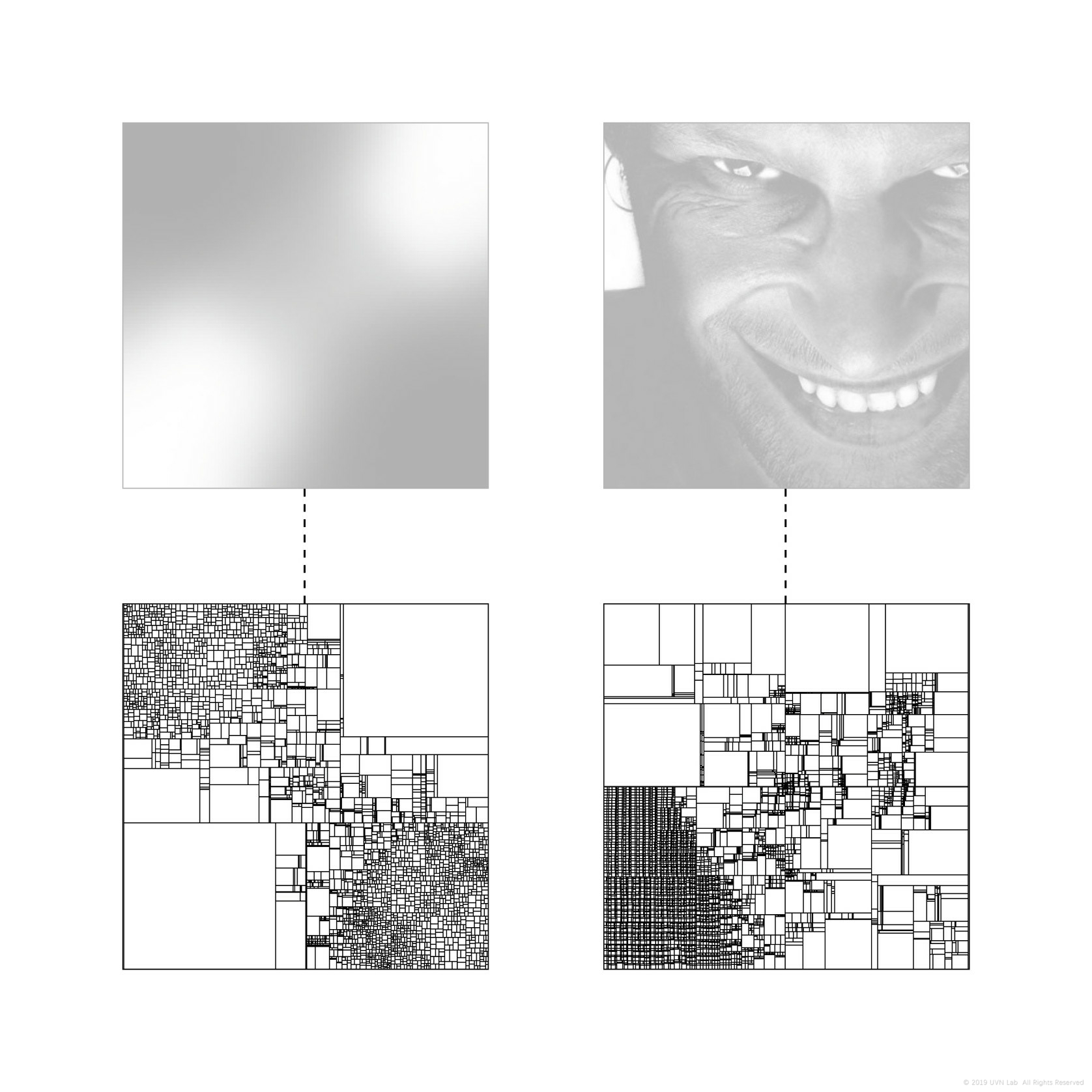
在这一阶段的研究中,为了缩减每次循环搜查像素灰度值的计算量,采样密度随着区域的面积减少而降低,不过这也导致每次划分的位置并非完全精确。
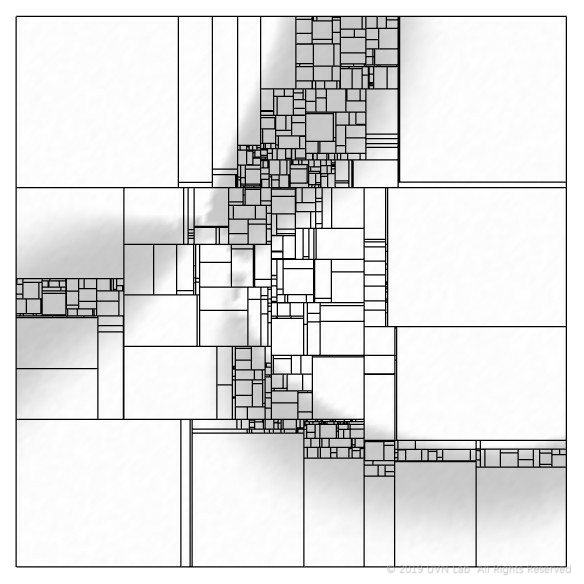
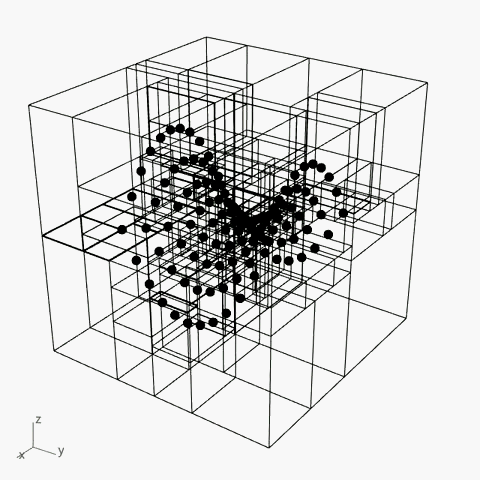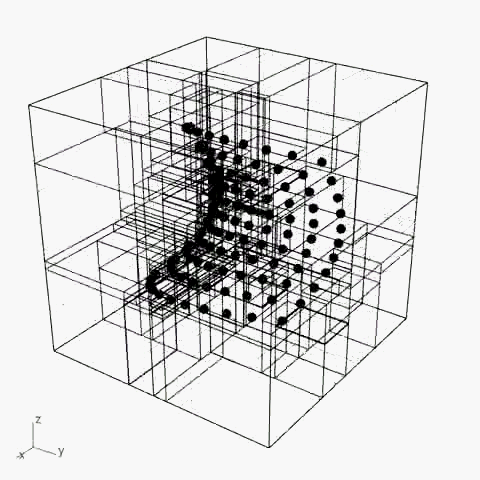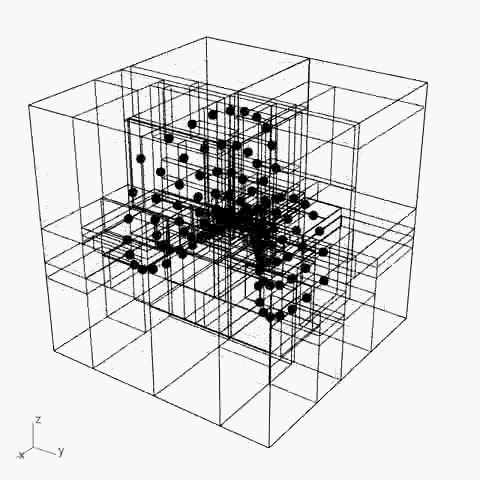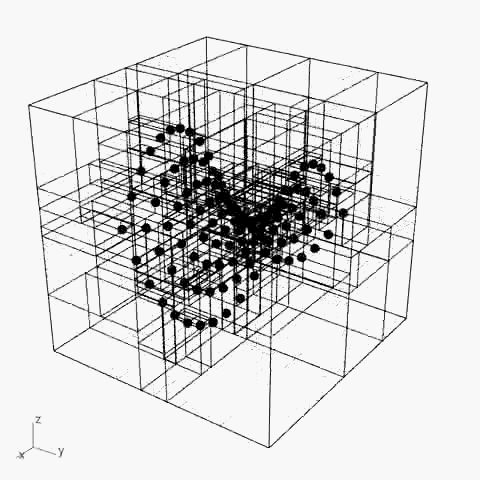
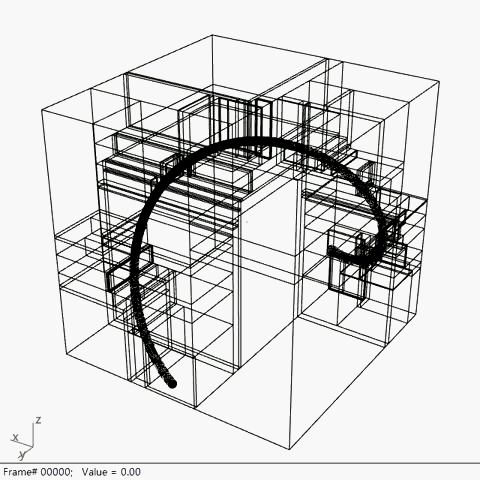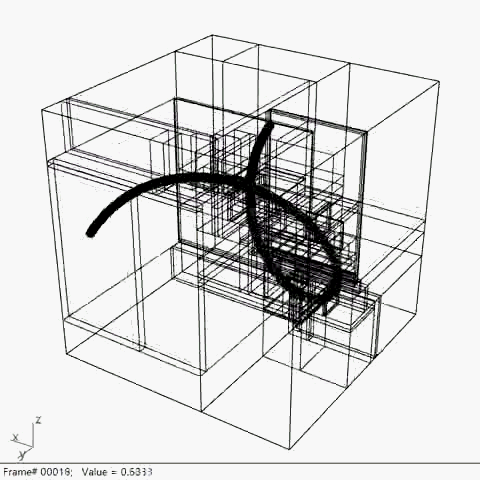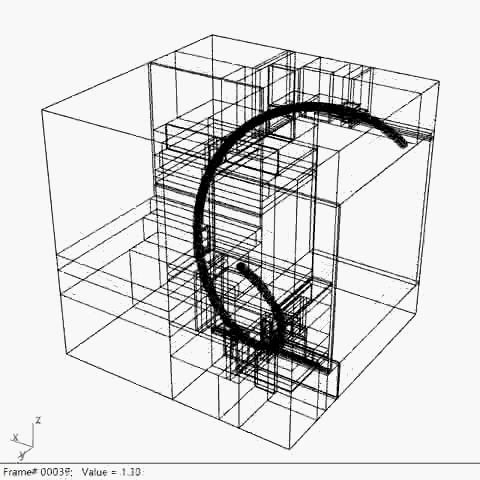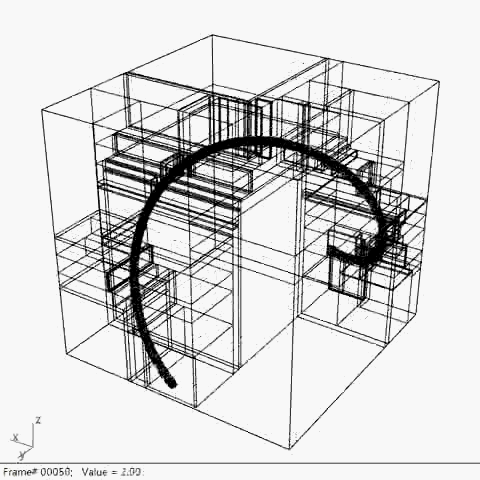
4. 点控制/ Point Based(K-D Tree)
最终阶段的研究采用了经典K-D Tree的逻辑
将点的集合作为空间划分的依据
并从2D的划分提升到3D空间
在此基础上,根据3D的模型形态进行空间划分具有了可行性